Difference between revisions of "ECE600 F13 Joint Distributions mhossain" - Rhea

Revision as of 14:21, 24 October 2013

Two Random Variables

We have been considering a single random variable X and introduces the pdf f$ _X $, and pmf p$ _X $, conditional pdf f$ _X $(x|M), the conditional pmf p$ _X $(x|M), pdf f$ _Y $ or pmf p$ _Y $ when Y = g(X), expectation E[g(X)], conditional expectation E[g(X)|M], and characteristic function $ \Phi_X $. We will now define similar tools for the case of two random variables X and Y.
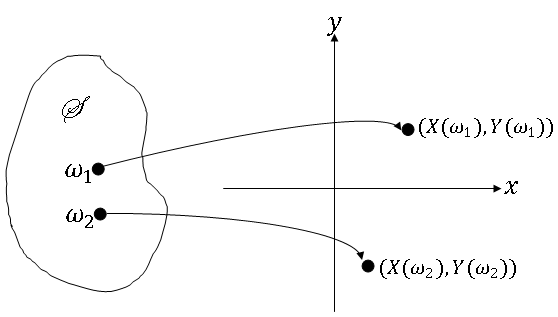
How do we define two random variables X,Y on a probability space (S,F,P)?

Fig 1: Mapping from S to X($ \omega $) and Y($ \omega $).

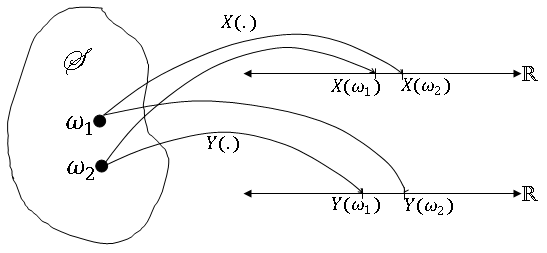
So two random variables can be viewed aw a mapping from S to R$ ^2 $, and (X,Y) is an ordered pair in R$ ^2 $. Note that we could draw the picture this way:

Fig 2: Mapping from S to X($ \omega $) and Y($ \omega $). Note that this model does not capture the joint behavior of X and Y and is hence incomplete.

but this would not capture the joint behavior or X and Y. Note also that if X and Y are defined on two different probability spaces, those two spaces can be combined to create (S,F,P).

In order for X and Y to be a valid random variable pair, we will need to consider regions D ⊂ R$ ^2 $.

We need {(X,Y) ∈ O} ∈ F for any open rectangle O ⊂ R$ ^2 $, then {(X,Y) ∈ D} ∈ F ∀D ∈ B(R$ ^2 $).
But (X($ \omega $),Y($ \omega $)) ∈ O if X($ \omega $ ∈ A and Y($ \omega $ ∈ B for some A, B ∈ B(R), so {(X,Y) ∈ 0} = X$ ^{-1} $(A) ∩ Y$ ^{-1} $(B)
If X and Y are valid random variables then

So,

So how do we find P((X,Y) ∈ D) for D ∈ B(R$ ^2 $)?

We will use joint cdfs, pdfs, and pmfs.

Joint Cumulative Distribution Function

Knowledge of F$ _X $(x) and F$ _Y $(y) alone will not be sufficient to compute P((X,Y) ∈ D) ∀D ∈ B(R$ ^2 $), in general.

Definition $ \qquad $ The joint cumulative distribution function of random variables X,Y defined on (S,F,P) is F$ _{XY} $(x,y) ≡ P({X ≤ x}{Y ≤ y}) for x,y ∈ R.
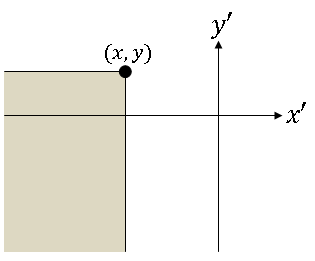
Note that in this case, D ≡ D$ _{XY} $ = {(x',y') ∈ R$ ^2 $: x' ≤ x, y' ≤ y}

Fig 3: The shaded region represents D

Properties of F$ _{XY} $: