Random Variables and Signals
Topic 13: Functions of Two Random Variables
One Function of Two Random Variables
Given random variables X and Y and a function g:R$ ^2 $→R, let Z = g(X,Y). What is f$ _Z $(z)?
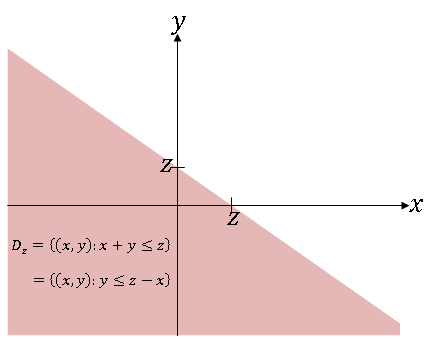
We assume that Z is a valid random variable, so that ∀z ∈ R, there is a D$ _z $ ∈ b(R$ ^2 $) such that
i.e.
Then,
and we can find f$ _Z $ from this.
Example $ \qquad $ g(x,y) = x + y. So Z = X + Y. Here,
and
If we now assume that X and Y are independent, then
Then,
So if X and Y are independent, and Z = X + Y, we can find f$ _Z $ by convolving f$ _X $ and f$ _Y $.
Example $ \qquad $