m (Protected "ECE600 F13 Functions of Two Random Variables mhossain" [edit=sysop:move=sysop]) |
|||
| (8 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category:ECE600]] | [[Category:ECE600]] | ||
[[Category:Lecture notes]] | [[Category:Lecture notes]] | ||
| + | [[ECE600_F13_notes_mhossain|Back to all ECE 600 notes]] | ||
| + | [[Category:ECE600]] | ||
| + | [[Category:probability]] | ||
| + | [[Category:lecture notes]] | ||
| + | [[Category:slecture]] | ||
<center><font size= 4> | <center><font size= 4> | ||
| − | '''Random Variables and Signals''' | + | [[ECE600_F13_notes_mhossain|'''The Comer Lectures on Random Variables and Signals''']] |
</font size> | </font size> | ||
| + | |||
| + | [https://www.projectrhea.org/learning/slectures.php Slectures] by [[user:Mhossain | Maliha Hossain]] | ||
| + | |||
<font size= 3> Topic 13: Functions of Two Random Variables</font size> | <font size= 3> Topic 13: Functions of Two Random Variables</font size> | ||
</center> | </center> | ||
| − | + | ---- | |
---- | ---- | ||
| Line 16: | Line 24: | ||
Given random variables X and Y and a function g:'''R'''<math>^2</math>→'''R''', let Z = g(X,Y). What is f<math>_Z</math>(z)? | Given random variables X and Y and a function g:'''R'''<math>^2</math>→'''R''', let Z = g(X,Y). What is f<math>_Z</math>(z)? | ||
| − | We assume that Z is a valid random variable, so that ∀z ∈ '''R''', there is a D<math>_z</math> ∈ | + | We assume that Z is a valid random variable, so that ∀z ∈ '''R''', there is a D<math>_z</math> ∈ B('''R'''<math>^2</math>) such that <br/> |
<center><math>\{Z\leq z\} = \{(X,Y)\in D_z\}</math></center> | <center><math>\{Z\leq z\} = \{(X,Y)\in D_z\}</math></center> | ||
i.e.<br/> | i.e.<br/> | ||
| Line 26: | Line 34: | ||
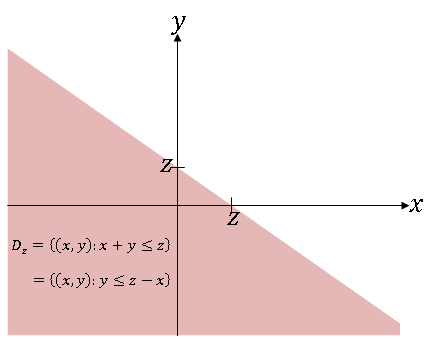
'''Example''' <math>\qquad</math> g(x,y) = x + y. So Z = X + Y. Here, <br/> | '''Example''' <math>\qquad</math> g(x,y) = x + y. So Z = X + Y. Here, <br/> | ||
| − | <center><math>D_z = \{(x,y)\in\ | + | <center><math>D_z = \{(x,y)\in\mathbb R^2:x+y\leq z\}</math><br/> |
and<br/> | and<br/> | ||
<math>F_Z(z) = \int_{-\infty}^{\infty}\int_{-\infty}^{z-x}f_{XY}(x,y)dydx</math></center> | <math>F_Z(z) = \int_{-\infty}^{\infty}\int_{-\infty}^{z-x}f_{XY}(x,y)dydx</math></center> | ||
| Line 42: | Line 50: | ||
Then, <br/> | Then, <br/> | ||
<center><math>\begin{align} | <center><math>\begin{align} | ||
| − | f_Z(z) &= \frac{d}{dz}[\int_{-\infty}^{\infty}f_X(x)F_Y(z-x)dx] \\ | + | f_Z(z) &= \frac{d}{dz}\left[\int_{-\infty}^{\infty}f_X(x)F_Y(z-x)dx\right] \\ |
&=\int_{-\infty}^{\infty}f_X(x)\frac{dF_Y(z-x)}{dz}dx \\ | &=\int_{-\infty}^{\infty}f_X(x)\frac{dF_Y(z-x)}{dz}dx \\ | ||
&=\int_{-\infty}^{\infty}f_X(x)f_Y(z-x)dx \\ | &=\int_{-\infty}^{\infty}f_X(x)f_Y(z-x)dx \\ | ||
| Line 52: | Line 60: | ||
'''Example''' <math>\qquad</math> X and Y are independent exponential random variables with means <math>\mu_X</math> = <math>\mu_Y</math> = <math>\mu</math>. So,<br/> | '''Example''' <math>\qquad</math> X and Y are independent exponential random variables with means <math>\mu_X</math> = <math>\mu_Y</math> = <math>\mu</math>. So,<br/> | ||
<center><math>\begin{align} | <center><math>\begin{align} | ||
| − | f_Z(z)&=\int_{-\infty}^{\infty}\frac{1}{\mu}e^{-\frac{x}{\mu}}u(x)\frac{1}{\mu}e^{-\frac{(z-x}{\mu}}u(z-x)dx \\ | + | f_Z(z)&=\int_{-\infty}^{\infty}\frac{1}{\mu}e^{-\frac{x}{\mu}}u(x)\frac{1}{\mu}e^{-\frac{(z-x)}{\mu}}u(z-x)dx \\ |
&=\int_0^z\frac{1}{\mu^2}e^{-\frac{z}{\mu}}dx\;\;\mbox{for}\;z=0 \\ | &=\int_0^z\frac{1}{\mu^2}e^{-\frac{z}{\mu}}dx\;\;\mbox{for}\;z=0 \\ | ||
&=\frac{z}{\mu^2}e^{-\frac{z}{\mu}}u(z) | &=\frac{z}{\mu^2}e^{-\frac{z}{\mu}}u(z) | ||
| Line 72: | Line 80: | ||
For example, if we have a linear transformation, then <br/> | For example, if we have a linear transformation, then <br/> | ||
| − | <center><math>\begin{bmatrix}Z\\W\end{bmatrix} =A \begin{bmatrix}X\\Y\end{bmatrix}</math></center> | + | <center><math>\begin{bmatrix}Z\\W\end{bmatrix} =\mathbf A \begin{bmatrix}X\\Y\end{bmatrix}</math></center> |
| − | where A is a 2x2 matrix. In this case, <br/> | + | where '''A''' is a 2x2 matrix. In this case, <br/> |
<center><math>\begin{align} | <center><math>\begin{align} | ||
g(x,y) &= a_{11}x+a_{12}y \\ | g(x,y) &= a_{11}x+a_{12}y \\ | ||
| Line 80: | Line 88: | ||
where <br/> | where <br/> | ||
| − | <center><math>A=\begin{bmatrix} | + | <center><math>\mathbf A=\begin{bmatrix} |
a_{11} & a_{12} \\ | a_{11} & a_{12} \\ | ||
a_{21} & a_{22} | a_{21} & a_{22} | ||
| Line 97: | Line 105: | ||
| − | ==Formula for Joint pdf f<math>ZW</math>== | + | ==Formula for Joint pdf f<math>_{ZW}</math>== |
Assume that the functions g and h satisfy | Assume that the functions g and h satisfy | ||
* z = g(x,y) and w = h(x,y) can be solved simultaneously for unique x and y. We will write x = g<math>^{-1}</math>(z,w) and y = h<math>^{-1}</math>(z,w) where g<math>^{-1}</math>:'''R'''<math>^2</math>→'''R''' and h<math>^{-1}</math>:'''R'''<math>^2</math>→'''R'''. | * z = g(x,y) and w = h(x,y) can be solved simultaneously for unique x and y. We will write x = g<math>^{-1}</math>(z,w) and y = h<math>^{-1}</math>(z,w) where g<math>^{-1}</math>:'''R'''<math>^2</math>→'''R''' and h<math>^{-1}</math>:'''R'''<math>^2</math>→'''R'''. | ||
| − | :For the linear transformation example, this means we assume A<math>^{-1}</math> exists (i.e. it is invertible). In this case <br/> | + | :For the linear transformation example, this means we assume '''A'''<math>^{-1}</math> exists (i.e. it is invertible). In this case <br/> |
<center><math>\begin{align} | <center><math>\begin{align} | ||
g^{-1}(z,w) &= b_{11}z+b_{12}w \\ | g^{-1}(z,w) &= b_{11}z+b_{12}w \\ | ||
| Line 107: | Line 115: | ||
\end{align}</math></center> | \end{align}</math></center> | ||
:where <br/> | :where <br/> | ||
| − | <center><math>A^{-1}=\begin{bmatrix} | + | <center><math>\mathbf A^{-1}=\begin{bmatrix} |
b_{11} & b_{12} \\ | b_{11} & b_{12} \\ | ||
b_{21} & b_{22} | b_{21} & b_{22} | ||
| Line 122: | Line 130: | ||
\begin{align} | \begin{align} | ||
\left|\frac{\partial(z,w)}{\partial(x,y)}\right| &\equiv | \left|\frac{\partial(z,w)}{\partial(x,y)}\right| &\equiv | ||
| − | \left|\begin{bmatrix} | + | \left|\mbox{det}\begin{bmatrix} |
\frac{\partial z}{\partial x} & \frac{\partial z}{\partial y} \\ | \frac{\partial z}{\partial x} & \frac{\partial z}{\partial y} \\ | ||
\frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} \end{bmatrix}\right| \\ | \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} \end{bmatrix}\right| \\ | ||
&= \left|\frac{\partial z}{\partial x}\frac{\partial w}{\partial y}-\frac{\partial z}{\partial y}\frac{\partial w}{\partial x} \right| | &= \left|\frac{\partial z}{\partial x}\frac{\partial w}{\partial y}-\frac{\partial z}{\partial y}\frac{\partial w}{\partial x} \right| | ||
\end{align}</math></center> | \end{align}</math></center> | ||
| − | <center><math>z=g(x,y)\qquad | + | <center><math>z=g(x,y)\qquad w=h(x,y)</math></center> |
Note that we take the absolute value of the determinant. This is called the Jacobian of the transformation. For more on the Jacobian, see [[Jacobian|here]]. | Note that we take the absolute value of the determinant. This is called the Jacobian of the transformation. For more on the Jacobian, see [[Jacobian|here]]. | ||
| Line 134: | Line 142: | ||
| − | '''Example''' X and Y are iid (independent and identically distributed) Gaussian random variables with <math>\mu_X=\mu_Y=\mu = 0</math>, <math>\sigma^2</math><math>_X</math>=<math>\sigma^2</math><math>_Y</math>=<math>\sigma^2</math> and r = 0. Then, br/> | + | '''Example''' X and Y are iid (independent and identically distributed) Gaussian random variables with <math>\mu_X=\mu_Y=\mu = 0</math>, <math>\sigma^2</math><math>_X</math>=<math>\sigma^2</math><math>_Y</math>=<math>\sigma^2</math> and r = 0. Then, <br/> |
<center><math>f_{XY}(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}</math></center> | <center><math>f_{XY}(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}</math></center> | ||
Let<br/> | Let<br/> | ||
| Line 152: | Line 160: | ||
where <br/> | where <br/> | ||
<center><math>\begin{align} | <center><math>\begin{align} | ||
| − | \left|\frac{\partial(x,y)}{\partial(r,\theta)}\right| &= \left|\begin{bmatrix} | + | \left|\frac{\partial(x,y)}{\partial(r,\theta)}\right| &= \left|\mbox{det}\begin{bmatrix} |
\frac{\partial x}{\partial r} & \frac{\partial x}{\partial\theta} \\ | \frac{\partial x}{\partial r} & \frac{\partial x}{\partial\theta} \\ | ||
\frac{\partial y}{\partial r} & \frac{\partial y}{\partial\theta} | \frac{\partial y}{\partial r} & \frac{\partial y}{\partial\theta} | ||
Latest revision as of 12:12, 21 May 2014
The Comer Lectures on Random Variables and Signals
Topic 13: Functions of Two Random Variables
Contents
One Function of Two Random Variables
Given random variables X and Y and a function g:R$ ^2 $→R, let Z = g(X,Y). What is f$ _Z $(z)?
We assume that Z is a valid random variable, so that ∀z ∈ R, there is a D$ _z $ ∈ B(R$ ^2 $) such that
i.e.
Then,
and we can find f$ _Z $ from this.
Example $ \qquad $ g(x,y) = x + y. So Z = X + Y. Here,
and
If we now assume that X and Y are independent, then
Then,
So if X and Y are independent, and Z = X + Y, we can find f$ _Z $ by convolving f$ _X $ and f$ _Y $.
Example $ \qquad $ X and Y are independent exponential random variables with means $ \mu_X $ = $ \mu_Y $ = $ \mu $. So,
So the sum of two independent exponential random variables is not an exponential random variable.
Two Functions of Two Random Variables
Given two random variables X and Y, cobsider random variables Z and W defined as follows:
where g:R$ ^2 $→R and h:R$ ^2 $→R.
For example, if we have a linear transformation, then
where A is a 2x2 matrix. In this case,
where
How do we find f$ _{ZW} $?
If we could find D$ _{z,w} $ = {(x,y) ∈ R$ ^2 $: g(x,y) ≤ z and h(x,y) ≤ w} for every (z,w) ∈ R$ ^2 $, then we could compute
It is often quite difficult to find D$ _{z,w} $, so we use a formula for f$ _{ZW} $ instead.
Formula for Joint pdf f$ _{ZW} $
Assume that the functions g and h satisfy
- z = g(x,y) and w = h(x,y) can be solved simultaneously for unique x and y. We will write x = g$ ^{-1} $(z,w) and y = h$ ^{-1} $(z,w) where g$ ^{-1} $:R$ ^2 $→R and h$ ^{-1} $:R$ ^2 $→R.
- For the linear transformation example, this means we assume A$ ^{-1} $ exists (i.e. it is invertible). In this case
- where
- The partial derivatives
- exist.
Then it can be shown that
where
Note that we take the absolute value of the determinant. This is called the Jacobian of the transformation. For more on the Jacobian, see here.
The proof for the above formula is in Papoulis.
Example X and Y are iid (independent and identically distributed) Gaussian random variables with $ \mu_X=\mu_Y=\mu = 0 $, $ \sigma^2 $$ _X $=$ \sigma^2 $$ _Y $=$ \sigma^2 $ and r = 0. Then,
Let
So,
Now use
where
We can then find the pdf of R from
This is the Rayleigh pdf.
Auxiliary Variables
If Z=g(X,Y), we can define another random variable W, find f$ _{ZW} $, and then integrate to get f$ _Z $. We call W an "auxiliary" or "dummy" variable. We should select h(x,y) so that the solution for f$ _Z $ is as simple as possible when we let W=h(X,Y). For the polar coordinate problem in the previous example, h(x,y) = tan$ ^{-1} $(y/x) works well for finding f$ _R $. Often, W = X works well since
References
- M. Comer. ECE 600. Class Lecture. Random Variables and Signals. Faculty of Electrical Engineering, Purdue University. Fall 2013.
Questions and comments
If you have any questions, comments, etc. please post them on this page