Line 54: Line 54:
 
'''Example''' <math>\qquad</math> X and Y are independent exponential random variables with means <math>\mu_X</math> = <math>\mu_Y</math> = <math>\mu</math>. So,<br/>
 
'''Example''' <math>\qquad</math> X and Y are independent exponential random variables with means <math>\mu_X</math> = <math>\mu_Y</math> = <math>\mu</math>. So,<br/>
 
<center><math>\begin{align}
 
<center><math>\begin{align}
−
f_Z(z)&=\int_{-\infty}^{\infty}\frac{1}{\mu}e^{-\frac{x}{\mu}}u(x)\frac{1}{\mu}e^{-\frac{(z-x}{\mu}}u(z-x)dx \\
+
f_Z(z)&=\int_{-\infty}^{\infty}\frac{1}{\mu}e^{-\frac{x}{\mu}}u(x)\frac{1}{\mu}e^{-\frac{(z-x)}{\mu}}u(z-x)dx \\
 
&=\int_0^z\frac{1}{\mu^2}e^{-\frac{z}{\mu}}dx\;\;\mbox{for}\;z=0 \\
 
&=\int_0^z\frac{1}{\mu^2}e^{-\frac{z}{\mu}}dx\;\;\mbox{for}\;z=0 \\
 
&=\frac{z}{\mu^2}e^{-\frac{z}{\mu}}u(z)
 
&=\frac{z}{\mu^2}e^{-\frac{z}{\mu}}u(z)
Line 75: Line 75:
 
For example, if we have a linear transformation, then <br/>
 
For example, if we have a linear transformation, then <br/>
 
<center><math>\begin{bmatrix}Z\\W\end{bmatrix} =A \begin{bmatrix}X\\Y\end{bmatrix}</math></center>
 
<center><math>\begin{bmatrix}Z\\W\end{bmatrix} =A \begin{bmatrix}X\\Y\end{bmatrix}</math></center>
−
  where A is a 2x2 matrix. In this case, <br/>
+
  where '''A''' is a 2x2 matrix. In this case, <br/>
 
<center><math>\begin{align}
 
<center><math>\begin{align}
 
g(x,y) &= a_{11}x+a_{12}y \\
 
g(x,y) &= a_{11}x+a_{12}y \\
Line 82: Line 82:
  
 
where <br/>
 
where <br/>
−
<center><math>A=\begin{bmatrix}
+
<center><math>\mathbf A=\begin{bmatrix}
 
a_{11} & a_{12} \\
 
a_{11} & a_{12} \\
 
a_{21} & a_{22}
 
a_{21} & a_{22}
Line 99: Line 99:
  
  
−
==Formula for Joint pdf f<math>ZW</math>==
+
==Formula for Joint pdf f<math>_{ZW}</math>==
  
 
Assume that the functions g and h satisfy
 
Assume that the functions g and h satisfy
 
* z = g(x,y) and w = h(x,y) can be solved simultaneously for unique x and y. We will write x = g<math>^{-1}</math>(z,w) and y = h<math>^{-1}</math>(z,w) where g<math>^{-1}</math>:'''R'''<math>^2</math>→'''R''' and h<math>^{-1}</math>:'''R'''<math>^2</math>→'''R'''.
 
* z = g(x,y) and w = h(x,y) can be solved simultaneously for unique x and y. We will write x = g<math>^{-1}</math>(z,w) and y = h<math>^{-1}</math>(z,w) where g<math>^{-1}</math>:'''R'''<math>^2</math>→'''R''' and h<math>^{-1}</math>:'''R'''<math>^2</math>→'''R'''.
−
:For the linear transformation example, this means we assume A<math>^{-1}</math> exists (i.e. it is invertible). In this case <br/>
+
:For the linear transformation example, this means we assume '''A'''<math>^{-1}</math> exists (i.e. it is invertible). In this case <br/>
 
<center><math>\begin{align}
 
<center><math>\begin{align}
 
g^{-1}(z,w) &= b_{11}z+b_{12}w \\
 
g^{-1}(z,w) &= b_{11}z+b_{12}w \\
Line 109: Line 109:
 
\end{align}</math></center>
 
\end{align}</math></center>
 
:where <br/>
 
:where <br/>
−
<center><math>A^{-1}=\begin{bmatrix}
+
<center><math>\mathbf A^{-1}=\begin{bmatrix}
 
b_{11} & b_{12} \\
 
b_{11} & b_{12} \\
 
b_{21} & b_{22}
 
b_{21} & b_{22}

Revision as of 19:58, 12 November 2013

Back to all ECE 600 notes


Random Variables and Signals

Topic 13: Functions of Two Random Variables


One Function of Two Random Variables

Given random variables X and Y and a function g:R$ ^2 $→R, let Z = g(X,Y). What is f$ _Z $(z)?

We assume that Z is a valid random variable, so that ∀z ∈ R, there is a D$ _z $ ∈ B(R$ ^2 $) such that

$ \{Z\leq z\} = \{(X,Y)\in D_z\} $

i.e.

$ D_z = \{(x,y)\in\mathbb R^2:g(x,y)\leq z\} $

Then,

$ F_Z(z) = P((X,Y)\in D_z)=\int\int_{D_z}f_{XY}(x,y)dxdy $

and we can find f$ _Z $ from this.

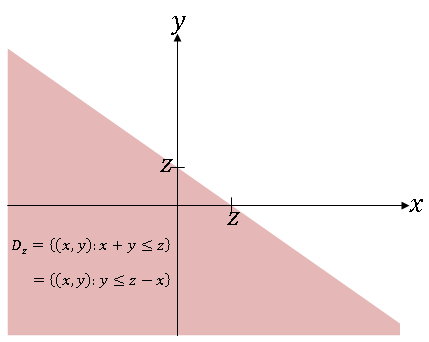
Example $ \qquad $ g(x,y) = x + y. So Z = X + Y. Here,

$ D_z = \{(x,y)\in\mathbf R^2:x+y\leq z\} $

and

$ F_Z(z) = \int_{-\infty}^{\infty}\int_{-\infty}^{z-x}f_{XY}(x,y)dydx $


Fig 1: The shaded region indicates D$ _z $.


If we now assume that X and Y are independent, then

$ \begin{align} F_Z(z) &= \int_{-\infty}^{\infty}\int_{-\infty}^{z-x}f_X(x)f_Y(y)dydx \\ &=\int_{-\infty}^{\infty}f_X(x)F_Y(z-x)dx \end{align} $

Then,

$ \begin{align} f_Z(z) &= \frac{d}{dz}\left[\int_{-\infty}^{\infty}f_X(x)F_Y(z-x)dx\right] \\ &=\int_{-\infty}^{\infty}f_X(x)\frac{dF_Y(z-x)}{dz}dx \\ &=\int_{-\infty}^{\infty}f_X(x)f_Y(z-x)dx \\ &=(f_X\ast f_Y)(z) \end{align} $

So if X and Y are independent, and Z = X + Y, we can find f$ _Z $ by convolving f$ _X $ and f$ _Y $.

Example $ \qquad $ X and Y are independent exponential random variables with means $ \mu_X $ = $ \mu_Y $ = $ \mu $. So,

$ \begin{align} f_Z(z)&=\int_{-\infty}^{\infty}\frac{1}{\mu}e^{-\frac{x}{\mu}}u(x)\frac{1}{\mu}e^{-\frac{(z-x)}{\mu}}u(z-x)dx \\ &=\int_0^z\frac{1}{\mu^2}e^{-\frac{z}{\mu}}dx\;\;\mbox{for}\;z=0 \\ &=\frac{z}{\mu^2}e^{-\frac{z}{\mu}}u(z) \end{align} $

So the sum of two independent exponential random variables is not an exponential random variable.


Two Functions of Two Random Variables

Given two random variables X and Y, cobsider random variables Z and W defined as follows:

$ \begin{align} Z &= g(X,Y) \\ W &= h(X,Y) \end{align} $

where g:R$ ^2 $→R and h:R$ ^2 $→R.

For example, if we have a linear transformation, then

$ \begin{bmatrix}Z\\W\end{bmatrix} =A \begin{bmatrix}X\\Y\end{bmatrix} $
where A is a 2x2 matrix. In this case,
$ \begin{align} g(x,y) &= a_{11}x+a_{12}y \\ h(x,y) &= a_{21}x+a_{22}y \end{align} $

where

$ \mathbf A=\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} $

How do we find f$ _{ZW} $?

If we could find D$ _{z,w} $ = {(x,y) ∈ R$ ^2 $: g(x,y) ≤ z and h(x,y) ≤ w} for every (z,w) ∈ R$ ^2 $, then we could compute

$ \begin{align} F_{ZW}(z,w) &= p(Z\leq z, W\leq w) \\ &=P((X,Y)\in D_{z,w}) \\ &=\int\int_{D_{z,w}}f_{XY}(x,y)dxdy \end{align} $

It is often quite difficult to find D$ _{z,w} $, so we use a formula for f$ _{ZW} $ instead.


Formula for Joint pdf f$ _{ZW} $

Assume that the functions g and h satisfy

  • z = g(x,y) and w = h(x,y) can be solved simultaneously for unique x and y. We will write x = g$ ^{-1} $(z,w) and y = h$ ^{-1} $(z,w) where g$ ^{-1} $:R$ ^2 $→R and h$ ^{-1} $:R$ ^2 $→R.
For the linear transformation example, this means we assume A$ ^{-1} $ exists (i.e. it is invertible). In this case
$ \begin{align} g^{-1}(z,w) &= b_{11}z+b_{12}w \\ h^{-1}(z,w) &= b_{21}z+b_{22}w \end{align} $
where
$ \mathbf A^{-1}=\begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} $
  • The partial derivatives
$ \frac{\partial x}{\partial z},\;\frac{\partial x}{\partial w},\;\frac{\partial y}{\partial z},\;\frac{\partial y}{\partial w},\;\frac{\partial z}{\partial x},\;\frac{\partial z}{\partial y},\;\frac{\partial w}{\partial x},\;\frac{\partial w}{\partial y} $
exist.

Then it can be shown that

$ f_{ZW}(z,w) = \frac{f_{XY}(g^{-1}(z,w),h^{-1}(z,w))}{\left|\frac{\partial\left(z,w\right)}{\partial\left(x,y\right)}\right|} $

where

$ \begin{align} \left|\frac{\partial(z,w)}{\partial(x,y)}\right| &\equiv \left|\begin{bmatrix} \frac{\partial z}{\partial x} & \frac{\partial z}{\partial y} \\ \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} \end{bmatrix}\right| \\ &= \left|\frac{\partial z}{\partial x}\frac{\partial w}{\partial y}-\frac{\partial z}{\partial y}\frac{\partial w}{\partial x} \right| \end{align} $
$ z=g(x,y)\qquad x=h(x,y) $

Note that we take the absolute value of the determinant. This is called the Jacobian of the transformation. For more on the Jacobian, see here.

The proof for the above formula is in Papoulis.


Example X and Y are iid (independent and identically distributed) Gaussian random variables with $ \mu_X=\mu_Y=\mu = 0 $, $ \sigma^2 $$ _X $=$ \sigma^2 $$ _Y $=$ \sigma^2 $ and r = 0. Then, br/>

$ f_{XY}(x,y)=\frac{1}{2\pi\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}} $

Let

$ R = \sqrt{X^2+Y^2}\qquad \Theta=\tan^{-1}\left(\frac{Y}{X}\right) $

So,

$ \begin{align} g(x,y) &= \sqrt{x^2+y^2} \\ h(x,y) &= \tan^{-1}\left(\frac{y}{x}\right) \\ g^{-1}(r,\theta)&=r\cos\theta \\ h^{-1}(r,\theta)&=r\sin\theta \end{align} $

Now use

$ f_{R\Theta}(r,\theta)=f_{XY}(g^{-1}(r,\theta),h^{-1}(r,\theta))\left|\frac{\partial(x,y)}{\partial(r,\theta)}\right| $

where

$ \begin{align} \left|\frac{\partial(x,y)}{\partial(r,\theta)}\right| &= \left|\begin{bmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial\theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial\theta} \end{bmatrix}\right| \\ \\ &=\left|\mbox{det}\begin{bmatrix} \cos\theta & -r\sin\theta \\ \sin\theta & r\cos\theta \end{bmatrix}\right| \\ \\ &=|r\cos^2\theta+r\sin^2\theta| \\ &=r \end{align} $


$ \begin{align} f_{R\Theta}(r,\theta) &=\frac{1}{2\pi\sigma^2}e^{-\frac{r^2\cos^2\theta+r^2\sin^2\theta}{2\sigma^2}}r\cdot u(r) \\ \\ &=\frac{r}{2\pi\sigma^2}e^{-\frac{r^2}{2\sigma^2}}u(r)\qquad -\pi\leq\theta\leq\pi \end{align} $

We can then find the pdf of R from

$ \begin{align} f_R(r) &= \int_{-\infty}^{\infty}f_{R,\Theta}(r,\theta)d\theta \\ &= \frac{r}{\sigma^2}e^{-\frac{r^2}{2\sigma^2}}u(r) \end{align} $

This is the Rayleigh pdf.


Auxiliary Variables

If Z=g(X,Y), we can define another random variable W, find f$ _{ZW} $, and then integrate to get f$ _Z $. We call W an "auxiliary" or "dummy" variable. We should select h(x,y) so that the solution for f$ _Z $ is as simple as possible when we let W=h(X,Y). For the polar coordinate problem in the previous example, h(x,y) = tan$ ^{-1} $(y/x) works well for finding f$ _R $. Often, W = X works well since

$ \frac{\delta w}{\delta x}=1 \qquad \frac{\delta y}{\delta w}=0 $


References


Questions and comments

If you have any questions, comments, etc. please post them on this page


Back to all ECE 600 notes

Retrieved from "https://www.projectrhea.org/rhea/index.php?title=ECE600_F13_Functions_of_Two_Random_Variables_mhossain&oldid=60122"
Shortcuts
Help Main Wiki Page Random Page Special Pages Log in
Search

Alumni Liaison

BSEE 2004, current Ph.D. student researching signal and image processing.

Landis Huffman