(New page: There are two methods for estimating parameters that are the center of a heated debate within the pattern recognition community. These methods are Maximum Likelihood Estimation (MLE) and ...) |
|||
| (8 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | =Comparison of MLE and Bayesian Parameter Estimation= | ||
| + | for [[ECE662:BoutinSpring08_Old_Kiwi|ECE662: Decision Theory]] | ||
| + | |||
| + | Complement to [[Lecture_7_-_MLE_and_BPE_OldKiwi|Lecture 7: Maximum Likelihood Estimation and Bayesian Parameter Estimation]], [[ECE662]], Spring 2010, Prof. Boutin | ||
| + | ---- | ||
There are two methods for estimating parameters that are the center of a heated debate within the pattern recognition community. These methods are Maximum Likelihood Estimation (MLE) and Bayesian parameter estimation. Despite the difference in theory between these two methods, they are quite similar when they are applied in practice. | There are two methods for estimating parameters that are the center of a heated debate within the pattern recognition community. These methods are Maximum Likelihood Estimation (MLE) and Bayesian parameter estimation. Despite the difference in theory between these two methods, they are quite similar when they are applied in practice. | ||
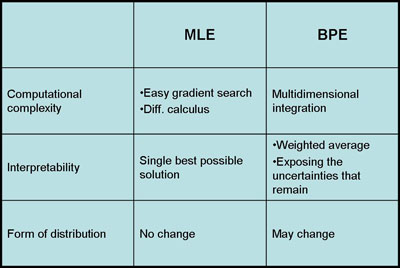
Maximum Likelihood (ML) and Bayesian parameter estimation make very different assumptions. Here the assumptions are contrasted briefly: | Maximum Likelihood (ML) and Bayesian parameter estimation make very different assumptions. Here the assumptions are contrasted briefly: | ||
| − | MLE | + | *'''MLE''' |
| + | |||
1) Deterministic (single, non-random) estimate of parameters, theta_ML | 1) Deterministic (single, non-random) estimate of parameters, theta_ML | ||
| Line 14: | Line 20: | ||
5) Overfitting solved with regularization parameters | 5) Overfitting solved with regularization parameters | ||
| − | Bayes | + | *'''Bayes''' |
1) Probabilistic (probability density) estimate of parameters, p(theta | Data) | 1) Probabilistic (probability density) estimate of parameters, p(theta | Data) | ||
| Line 27: | Line 33: | ||
In the end, both methods require a parameter to avoid overfitting. The parameter used in Maximum Likelihood Estimation is not as intellectually satisfying, because it does not arise as naturally from the derivation. However, even with Bayesian likelihood it is difficult to justify a given prior. For example, what is a "typical" standard deviation for a Gaussian distribution? | In the end, both methods require a parameter to avoid overfitting. The parameter used in Maximum Likelihood Estimation is not as intellectually satisfying, because it does not arise as naturally from the derivation. However, even with Bayesian likelihood it is difficult to justify a given prior. For example, what is a "typical" standard deviation for a Gaussian distribution? | ||
| + | |||
| + | *'''Comparison table between MLE and BPE''' | ||
| + | [[Image:MLEvBPE comparison_Old Kiwi.jpg]] | ||
| + | |||
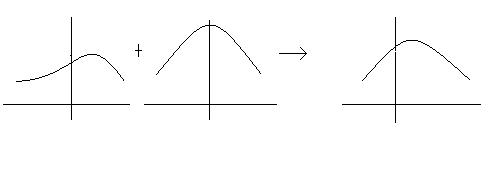
| + | *'''Illustration of BPE processes''' | ||
| + | [[Image:BPEprocess_Old Kiwi.jpg]] | ||
| + | ---- | ||
| + | Back to [[Lecture_7_-_MLE_and_BPE_OldKiwi|Lecture 7: Maximum Likelihood Estimation and Bayesian Parameter Estimation]], [[ECE662]], Spring 2010, Prof. Boutin | ||
Latest revision as of 10:39, 20 May 2013
Comparison of MLE and Bayesian Parameter Estimation
Complement to Lecture 7: Maximum Likelihood Estimation and Bayesian Parameter Estimation, ECE662, Spring 2010, Prof. Boutin
There are two methods for estimating parameters that are the center of a heated debate within the pattern recognition community. These methods are Maximum Likelihood Estimation (MLE) and Bayesian parameter estimation. Despite the difference in theory between these two methods, they are quite similar when they are applied in practice.
Maximum Likelihood (ML) and Bayesian parameter estimation make very different assumptions. Here the assumptions are contrasted briefly:
- MLE
1) Deterministic (single, non-random) estimate of parameters, theta_ML
2) Determining probability of a new point requires one calculation: P(x|theta)
3) No "prior knowledge"
4) Estimate of variance and other parameters is often biased
5) Overfitting solved with regularization parameters
- Bayes
1) Probabilistic (probability density) estimate of parameters, p(theta | Data)
2) Determining probability of a new point requires integration over the parameter space
3) Prior knowledge is necessary
4) With certain specially-designed priors, leads naturally to unbiased estimate of variance
5) Overfitting is solved by the selection of the prior
In the end, both methods require a parameter to avoid overfitting. The parameter used in Maximum Likelihood Estimation is not as intellectually satisfying, because it does not arise as naturally from the derivation. However, even with Bayesian likelihood it is difficult to justify a given prior. For example, what is a "typical" standard deviation for a Gaussian distribution?
- Comparison table between MLE and BPE
- Illustration of BPE processes
Back to Lecture 7: Maximum Likelihood Estimation and Bayesian Parameter Estimation, ECE662, Spring 2010, Prof. Boutin