Comparison of the DFT and FFT via Matrices
BY: Cary A. Wood
The purpose of this article is to illustrate the differences of the Discrete Fourier Transform (DFT) versus the Fast Fourier Transform (FFT). In addition, it will provide a further explanation of the FFT calculation path as described in Lab 6 (Week 2, pg. 5) of ECE 438. The link can be found here [1]. Please note the following explanation of the FFT will focus on the "divide and conquer" method and assume the user understands its basic concepts. Recursion, although important, will not be discussed.
To start, we will define the DFT as,
$ X_N[k] = \sum_{n=0}^{N-1} x[n] e^{-j2{\pi}kn/N} {\;} {\;} (Eq. 1) $
It is fairly easy to visualize this 1 point DFT, but how does it look when x[n] has 8 points, 1024 points, etc. That's where matrices come in. For an N point DFT, we will define our input as x[n] where n = 0, 1, 2, ... N-1. Similarly, the output will be defined as X[k] where k = 0, 1, 2, ... N-1. Referring to our definition of the Discrete Fourier Transform above, to compute an N point DFT, all we need to do is simply repeat Eq. 1, N times. For every value of x[n] in the discrete time domain, there is a corresponding value, X[k], in the frequency domain.
Input x[n] =
$ \begin{bmatrix} x[0] & x[1] & {\;}{\dotsb} & x[N-1] \end{bmatrix} $
Output X[k] =
$ \begin{bmatrix} X[0] \\ X[1] \\ {\vdots} \\ X[N-1] \end{bmatrix} $
To solve for X[K], means simply repeating Eq. 1, N times, where x[n] is a real scalar value for each entry. We represent this in the matrices below.
$ \begin{bmatrix} X[0] \\ X[1] \\ X[2] \\ {\vdots} \\ X[N-1] \end{bmatrix} = x[0]\begin{bmatrix} e^{-j2{\pi}(0)/N} \\ e^{-j2{\pi}(0)/N} \\ e^{-j2{\pi}(0)/N} \\ {\vdots} \\ e^{-j2{\pi}(0)/N} \end{bmatrix} + x[1]\begin{bmatrix} e^{-j2{\pi}(0)/N} \\ e^{-j2{\pi}(1)/N} \\ e^{-j2{\pi}(2)/N} \\ {\vdots} \\ e^{-j2{\pi}(N-1)/N} \end{bmatrix} + x[2]\begin{bmatrix} e^{-j2{\pi}(0)/N} \\ e^{-j2{\pi}(2)/N} \\ e^{-j2{\pi}(4)/N} \\ {\vdots} \\ e^{-j2{\pi}2(N-1)/N} \end{bmatrix} + {\;} {\dotsb} {\;} + x[N-1]\begin{bmatrix} e^{-j2{\pi}(0)/N} \\ e^{-j2{\pi}(N-1)/N} \\ e^{-j2{\pi}2(N-1)/N} \\ {\vdots} \\ e^{-j2{\pi}{(N-1)^2}/N} \end{bmatrix} {\;} {\;} (Eq. 2) $
From this matrix representation of the DFT, you can see that N^2 complex multiplications and N^2 - N complex additions are necessary to fully compute the discrete fourier transform. There are a few simplifications that can be made right away. The first column vector of complex exponentials can be reduced to a vector of 1's. This is possible because, e^(0*anything) will always equal 1. This also applies for the first entry in each vector of complex exponentials because n always begins at 0.
Now whats happens when we want to perform the DFT on 3 minute audio signal recorded at a 44.1 kHz sampling rate? Our handy-dandy DFT suddenly becomes extremely lengthy since computation time increases with a rate of N^2 + (N^2-N). Due to the work of Cooley and Turkey (although previously discovered by Gauss), the development of the Fast Fourier Transform has reduced computation time by orders of magnitude.
Introduction of the Fast Fourier Transform
To derive the FFT we will use the "divide and conquer" method as stated before. This means that we will divide Eq. 1 into two separate summations. The first summation processes the even components of x[n] while the second summation processes the odd components of x[n]. This produces,
$ X_N[k] = \sum_{m=0}^{{N/2}-1} x[2m] e^{-j2{\pi}k(m)/(N/2)} + e^{-j2{\pi}k/N}\sum_{m=0}^{{N/2}-1} x[2m+1] e^{-j2{\pi}k(m)/(N/2)} {\;} {\;} (Eq. 3) $
Our DFT has now been successfully split into two N/2 pt DFT's. For simplification purposes, the first summation will be defined as X0[k] and the second summation as X1[k]. We can now simplify Eq. 3 to the following form.
$ X[k] = X_0[k] + e^{-j2{\pi}k/n}X_1[k] {\;} {\;} {\;} (Eq. 4) $
The complex exponential preceding X1[k] in Eq. 3 is generally called the "twiddle factor" and represented by
$ {W_N}^k = e^{-j2{\pi}k/N} $
By definition of the discrete fourier transform, X0[k] and X1[k] are periodic with period N/2. Therefore we can split Eq. 3 into two separate equations.
$ X[k] = X_0[k] + {{W_N}^k}X_1[k] $
$ X[k+(N/2)] = X_0[k] - {{W_N}^k}X_1[k] $
Once again were are left with a number of 1 pt. DFT's. So how do represent this in matrix form? First, note that we have two separate equations and therefore need two separate equations of matrices. Similar to Eq. 2, we will repeat the DFT for the entire length of the input signal. However, since we split x[n] into even and odd components, we will only repeat the DFT (N/2) times for X0 and X1. The first equation solves for the first half of X[k].
Eq. 5 and 6,
$ \begin{bmatrix} \sum_{n=0}^{{N/2}-1} x(2m) \\ \sum_{n=0}^{{N/2}-1} x(2m)e^{-j2{\pi}(1)2m/(N/2)} \\ \sum_{n=0}^{{N/2}-1} x(2m)e^{-j2{\pi}(2)2m/(N/2)} \\ {\vdots} \\ \sum_{n=0}^{{N/2}-1} x(2m)e^{-j2{\pi}({N/2}-1)2m/(N/2)} \\ \end{bmatrix} + \begin{bmatrix} {W_N}^0 & 0 & {\dotsb} & 0 \\ 0 & {W_N}^1 & & {\vdots} \\ {\vdots} & & {W_N}^2 & \\ & & {\ddots} & 0 \\ 0 & {\dotsb} & & {W_N}^{(N/2)-1} \end{bmatrix} \begin{bmatrix} \sum_{n=0}^{{N/2}-1} x(2m+1) \\ \sum_{n=0}^{{N/2}-1} x(2m+1)e^{-j2{\pi}m/(N/2)} \\ \sum_{n=0}^{{N/2}-1} x(2m+1)e^{-j2{\pi}m/(N/2)} \\ {\vdots} \\ \sum_{n=0}^{{N/2}-1} x(2m+1)e^{-j2{\pi}m/(N/2)} \\ \end{bmatrix} = \begin{bmatrix} X[0] \\ X[1] \\ X[2] \\ {\vdots} \\ X[{N/2}-1] \end{bmatrix} $
The second equation solves for the second half of X[k].
$ \begin{bmatrix} \sum_{n=0}^{{N/2}-1} x(2m) \\ \sum_{n=0}^{{N/2}-1} x(2m)e^{-j2{\pi}(1)2m/(N/2)} \\ \sum_{n=0}^{{N/2}-1} x(2m)e^{-j2{\pi}(2)2m/(N/2)} \\ {\vdots} \\ \sum_{n=0}^{{N/2}-1} x(2m)e^{-j2{\pi}({N/2}-1)2m/(N/2)} \\ \end{bmatrix} - \begin{bmatrix} {W_N}^0 & 0 & {\dotsb} & 0 \\ 0 & {W_N}^1 & & {\vdots} \\ {\vdots} & & {W_N}^2 & \\ & & {\ddots} & 0 \\ 0 & {\dotsb} & & {W_N}^{(N/2)-1} \end{bmatrix} \begin{bmatrix} \sum_{n=0}^{{N/2}-1} x(2m+1) \\ \sum_{n=0}^{{N/2}-1} x(2m+1)e^{-j2{\pi}m/(N/2)} \\ \sum_{n=0}^{{N/2}-1} x(2m+1)e^{-j2{\pi}m/(N/2)} \\ {\vdots} \\ \sum_{n=0}^{{N/2}-1} x(2m+1)e^{-j2{\pi}m/(N/2)} \\ \end{bmatrix} = \begin{bmatrix} X[N/2] \\ X[(N/2)+1] \\ X[(N/2)+2] \\ {\vdots} \\ X[N-1] \end{bmatrix} $
After analyzing the two matrices above, there are a few concepts you should understand.
1) The matrix X0 in each equation is just the condensed form of Eq. 2 and then cut in half. It is simply the DFT repeated (N/2) times where the input is the even indices of x[n].
2) The matrix X1 in each equation, is also the condensed form of Eq. 2 cut in half. However, the input is now the odd indices of x[n].
The equations below are the same as Eq. 5 and 6, but X0 and X1 are expressed in a simplified format.
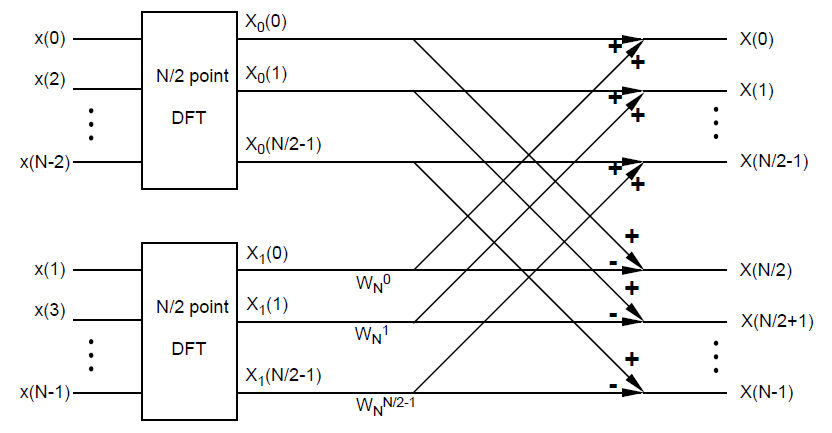
Now compare these two equations to the FFT signal path below, as shown in Week 2 of Lab 6.
As you can see from image above, X0 and X1 are only calculated one time. In conclusion, the signal path image in Lab 6 is derived directly from the matrix equations above (Eq. 5 and 6). Although matrices X0 and X1 are used in both equations, they only need to be calculated once. This is key to the Fast Fourier. Hopefully this gives you a better idea of how to visualize the map given above.