Bayesian Statistics
What is Bayesian Statistics?
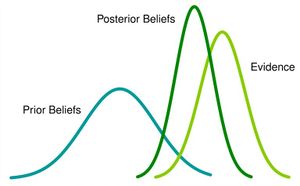
Bayesian statistics is a theory based on the Bayesian interpretation of probability where probability expresses a degree of belief in an event. This degree of belief might be based on prior knowledge of the event or on personal beliefs on the event. These methods use Bayes’ theorem to calculate and renew probabilities after obtaining new data. The theorem describes the conditional probability (probability of one event occurring with some relationship to one or more other events) based on data and prior beliefs or conditions related to the event.
Bayesian Statistics is centered around one major theorem named Bayes' Theorem. This theorem is used to update probabilities once new data is introduced. Bayes' Theorem is stated as: $ P(A | B) = \frac{P(B | A)P(A)}{P(B)} $ where A usually represents the proposition of the statement and B represents the evidence or new data. This theorem relates the probability of the hypothesis before getting the evidence to the probability of the hypothesis after getting the evidence, making P(A) the prior and P(B) the posterior, and the ratio of the two the likelihood ratio.