Applications:
1. Banach Algebras
Banach Spaces are utilized in another concept of mathematics created by the same Stefan Banach: Banach Algebras. To understand this concept, we must first understand the basics of algebras over a field. An algebra over a field is a type of vector space that can be generated from two other vector spaces, also called a bilinear product. A Banach Algebra is defined to be associative, that is, containing usable operations of addition, multiplication, and scalar multiplication. A Banach Algebra is itself a Banach Space.
2. Wiener Algebra
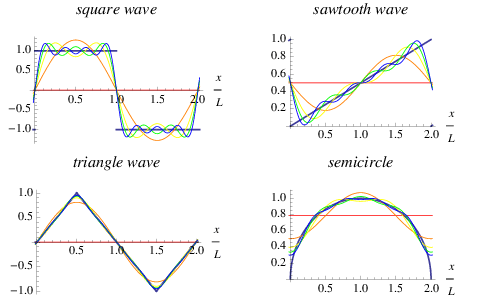
Another application of Banach Spaces can be found in the Wiener Algebra. The fundamental concept within Wiener Algebras lies in Fourier Series. A Fourier series is a type of series that repeats at regular intervals using summated sinusoidal functions. They are said to be periodic. Some examples of Fourier series can be seen below.
The Wiener Algebra is simply the set of all absolutely converging Fourier series. It also is a Banach Space.