| Line 15: | Line 15: | ||
As seen in the plot, the signal <math> X(f) </math> has a triangular shape and is band-limited by <math> f_{max} </math>. By the Nyquist-Shannon Sampling Theorem, the sampling frequency <math> f_{s1} </math> must be greater than <math> 2f_{max} </math>. For this discussion, assume <math> f_{s1} </math> is just slightly greater than <math> 2f_{max} </math>. | As seen in the plot, the signal <math> X(f) </math> has a triangular shape and is band-limited by <math> f_{max} </math>. By the Nyquist-Shannon Sampling Theorem, the sampling frequency <math> f_{s1} </math> must be greater than <math> 2f_{max} </math>. For this discussion, assume <math> f_{s1} </math> is just slightly greater than <math> 2f_{max} </math>. | ||
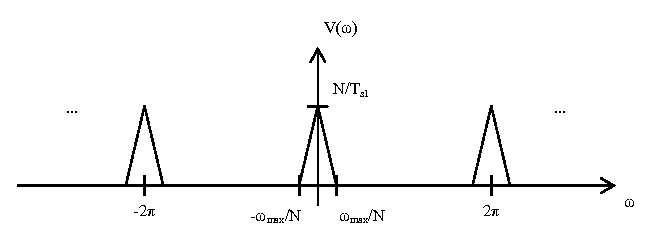
| − | Now, we are going to sample <math> x(t) </math> with an impulse train with period <math> T_{s1} = 1/f_{s1} </math> and convert to a discrete time signal. This has the affect of scaling the magnitude axis of <math> X(f) </math> by <math> 1/T_{s1} </math> and the frequency axis by <math> 2\pi T_{s1} </math>, and then repeating the result every <math> 2\pi </math>. This yields the following plot <math> X_d(\omega) </math>: | + | Now, we are going to sample <math> x(t) </math> with an impulse train with period <math> T_{s1} = 1/f_{s1} </math> and convert to a discrete time signal. This has the affect of scaling the magnitude axis of <math> X(f) </math> by <math> 1/T_{s1} </math> and the frequency axis by <math> 2\pi T_{s1} </math>, and then repeating the result every <math> \omega = 2\pi </math>. This yields the following plot <math> X_d(\omega) </math>: |
[[Image:Xd_w_plot.png]] | [[Image:Xd_w_plot.png]] | ||
== Without Up-sampling == | == Without Up-sampling == | ||
| + | |||
| + | First, consider the process of signal reconstruction without up-sampling. The following diagram shows the process: | ||
[[Image:Dac_diag.png]] | [[Image:Dac_diag.png]] | ||
| + | |||
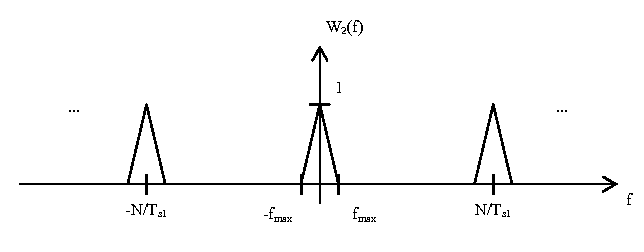
| + | The first block is a digital-to-analog converter. This converts the discrete time signal to a continuous time signal. This has the effect of scaling the magnitude axis by <math> T_{s1} </math> and the omega axis by <math> \frac{1}{2\pi T_{s1}} </math>. This yields the following plot: | ||
| + | |||
[[Image:W1_f_plot.png]] | [[Image:W1_f_plot.png]] | ||
Revision as of 18:09, 22 September 2009
Contents
Introduction
With microprocessors becoming ever increasingly faster, smaller, and cheaper, it is preferable to use digital signal processing as a way to compensate for distortions caused by analog circuitry. One area that this can be applied is in signal reconstruction, where a low pass analog filter is used on the output of a digital-to-analog converter to attenuate unwanted frequency components above the Nyquist frequency.
The problem with analog low pass filters is that higher the order, the more resistors, capacitors, and op-amps are required in its construction. More circuit components means more circuit board space, which is a precious commodity with today's hand-held devices.
Here, it will be explained how up-sampling can be used to relax requirements on analog low pass filter design while decreasing signal distortion.
A Representative DT Signal
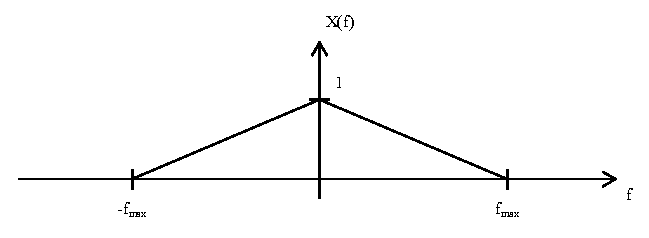
For this discussion, a representative signal $ x(t) $ will be used to demonstrate the process of signal reconstruction. We will look at the signal in the frequency domain, as shown in the plot below:
As seen in the plot, the signal $ X(f) $ has a triangular shape and is band-limited by $ f_{max} $. By the Nyquist-Shannon Sampling Theorem, the sampling frequency $ f_{s1} $ must be greater than $ 2f_{max} $. For this discussion, assume $ f_{s1} $ is just slightly greater than $ 2f_{max} $.
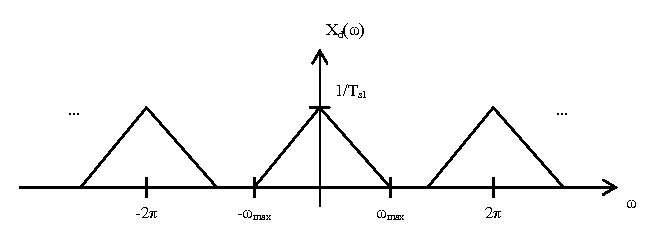
Now, we are going to sample $ x(t) $ with an impulse train with period $ T_{s1} = 1/f_{s1} $ and convert to a discrete time signal. This has the affect of scaling the magnitude axis of $ X(f) $ by $ 1/T_{s1} $ and the frequency axis by $ 2\pi T_{s1} $, and then repeating the result every $ \omega = 2\pi $. This yields the following plot $ X_d(\omega) $:
Without Up-sampling
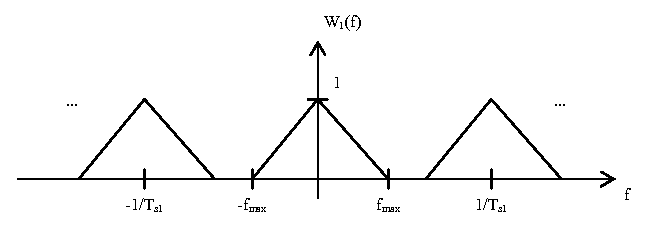
First, consider the process of signal reconstruction without up-sampling. The following diagram shows the process:
The first block is a digital-to-analog converter. This converts the discrete time signal to a continuous time signal. This has the effect of scaling the magnitude axis by $ T_{s1} $ and the omega axis by $ \frac{1}{2\pi T_{s1}} $. This yields the following plot: