Part 1
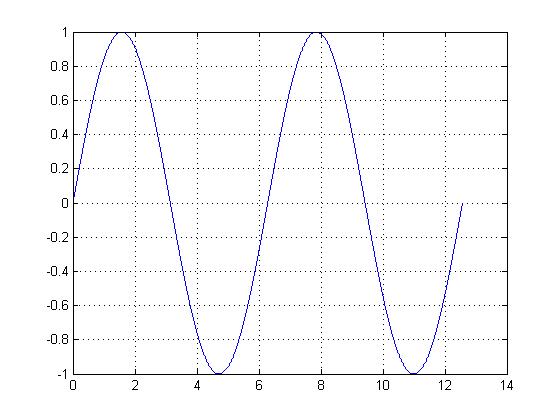
One can take a signal that would be periodic in continuous time and turn it into a signal that is not periodic in discrete time. Consider the continuous time signal $ x(t)=sin(t) $. Plotting this signal yields a smooth waveform that repeats itself with period $ T=2\pi $.
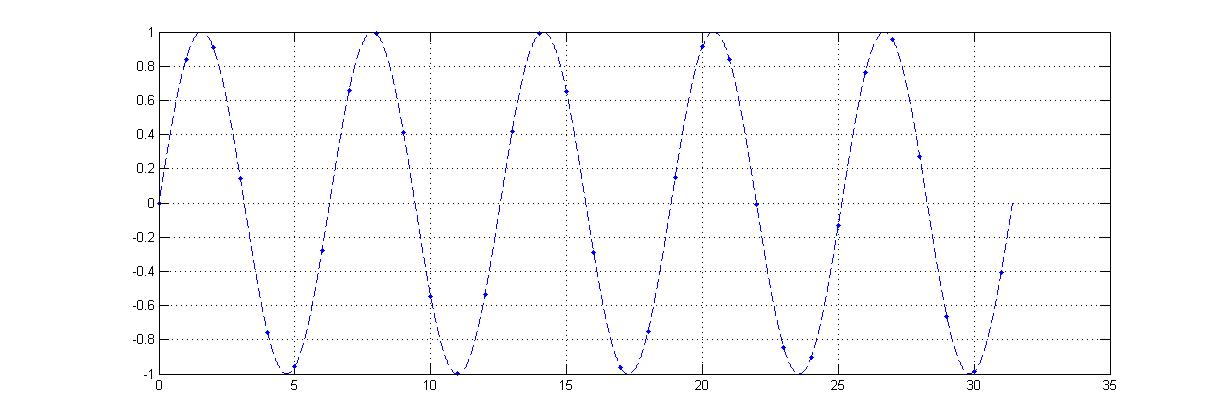
Sampling this signal at every integer time yields something altogether different.
The new discrete time function looks like this on its own.