Periodicity of Markov Chains
Let us denote $ d_{i} $ as the greatest common divisor of the number set $ {n:n\geq1, P_{ii}^{n}} $ ($ P_{ii}^{n} $ means the probability of state $ i $ recurring after $ n’s $ step); then, we can say $ d_{i} $ is the period of state $ i $. When $ d_{i} > 1 $, we say state $ i $ is a state with period; when $ d_{i} = 1 $, we say state $ i $ is a state without period.
This is easy to understand: if it takes 2, 4, 6 steps for state $ i $ to recur, we can see the period is 2 (the greatest common divisor of 2, 4, 6). On the other hand, if it takes 3, 7, 13 steps for state $ i $ to recur, the greatest common divisor is 1; therefore, it doesn’t have periodicity.
How do we distinguish whether a state is periodic or not? The easiest way is to use the two sufficient condition stated below:
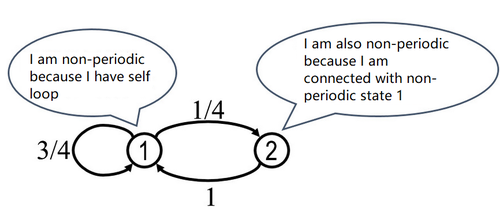
- If the state has a self-loop, then it must be non-periodic
- If one state is interoperable with another non-periodic state, then such state must be non-periodic.