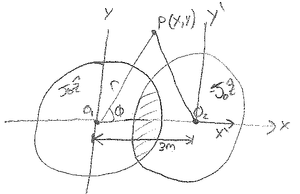
Using superposition
In the left cylinder
$ \begin{equation*} \nabla\times \bar{H}=\bar{J} \longrightarrow \oint \bar{H}\cdot d\bar{l}=\int_S\bar{J}\cdot d\bar{S} \qquad \left\{ \begin{aligned} dl&=dr\hat{r}+rd\phi\hat{\phi}+dz\hat{z}\\ d\bar{S}_z&=rd\phi dr\hat{z} \end{aligned} \right. \end{equation*} $
$ \begin{align*} \int_0^{2\pi}H_{\phi}(rd\phi)&=\int_0^r\int_0^{2\pi} J_0(r'd\phi dr')\\ H_{\phi}(2\pi r)&=2\pi J_0(\frac{r^2}{2}) \\ & \boxed{\bar{H}=\frac{J_0r}{2}\hat{\phi}} \end{align*} $
$ \begin{align*} \text{Transform to cartesian:}&\left\{\begin{aligned} r&=\sqrt{x^2+y^2}\\ \hat{\phi}&=-sin\phi\hat{x}+cos\phi\hat{y}\\ &=(\frac{-y}{\sqrt{x^2+y^2}})\hat{x}+(\frac{x}{\sqrt{x^2+y^2}})\hat{y} \end{aligned}\right. \\ & \boxed{\bar{H}_L=\frac{J_0}{2}\left[-y\hat{x}+x\hat{y}\right]} \end{align*} $
In the right cilinder
$ \begin{align*} &\bar{H}_R=\frac{-J_0}{2}\left[-y'\hat{x'}+x'\hat{y'}\right]& \left\{ \begin{aligned} x'&=x-3\\ y'&=y\\ \hat{x}'&=\hat{x}\\ \hat{y}'&=\hat{y} \end{aligned} \right.\\ &\boxed{\bar{H}_R=\frac{-J_0}{2}\left[-y\hat{x}+(x-3)\hat{y}\right]}& \end{align*} $
$ \begin{equation*} \boxed{\bar{H}_T=\bar{H}_L+\bar{H}_R=\frac{3J_0}{2}\hat{y}} \end{equation*} $

