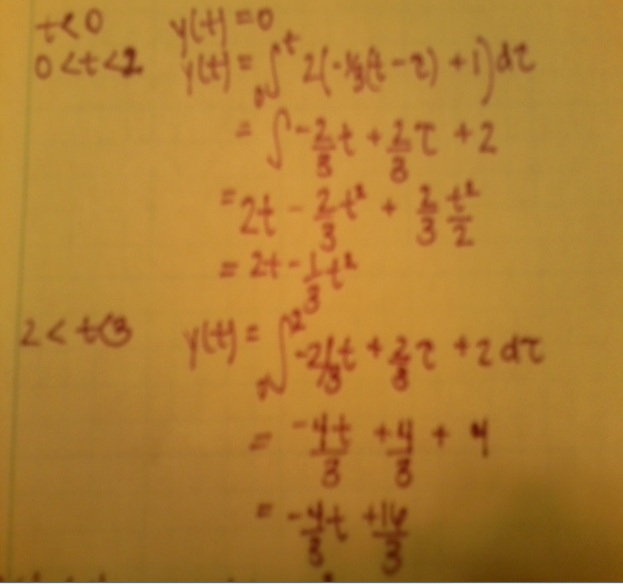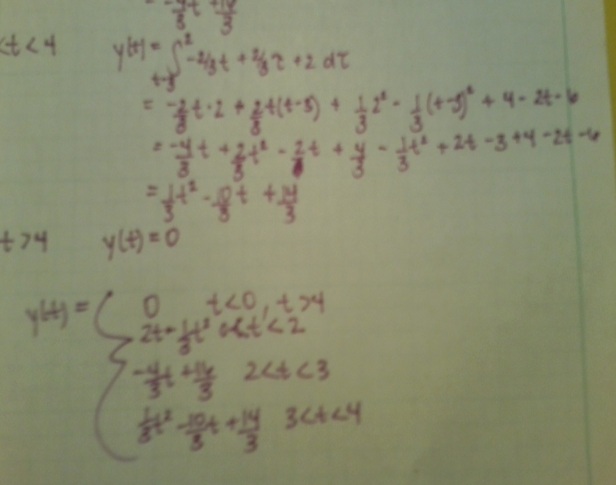EXTRA CREDIT
1. Linear and Non Linear
Linear example $ y[n] = 54x[n] $, $ h[n] = 62x[n] $, $ y[n] + h[n] = 54x[n] + 62x[n] $
Non Linear example $ y(t) =x^3(t) $, $ h(t) = x^3(t) $, $ y(t) + h(t) = (x(t)+x(t))^2 $ =\= $ x^2(t) +x^2(t) $
Causal and Non Causal
Causal example $ y[n]=70x[n-1] $ Non Causal example $ y[n]=76x[n+1] $
Memory and Memoryless
Memory example $ y[n]=x[n]+x[n-1] $ Memoryless example $ y[n]=36x[n] $
Invertible and noninvertible
Invertible example $ y(t)=5x(t) $ Nonivertible example $ y(t)=x^4(t) $
Stable and Nonstable
Stable example $ y(t)=sin(3t) $ Nonstable example $ y(t)=4e^3x(t) $
Time variant and Time invariant
Time variant example $ y(t)=3tx(t) $ Time Invariant example $ y(t)=3x(t) $
2.
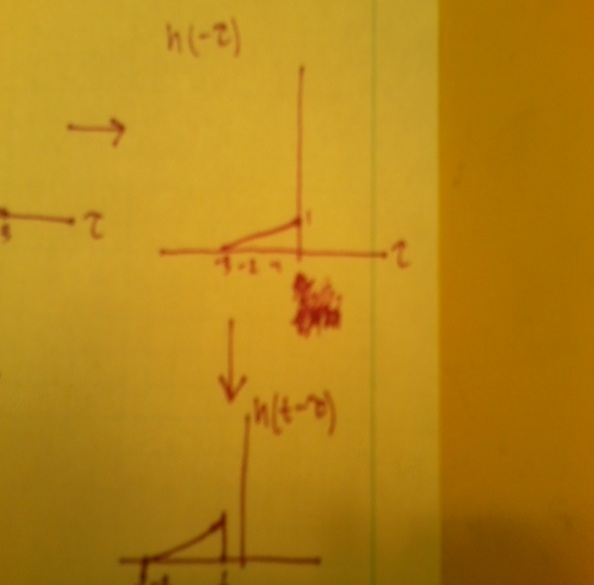
I apologize for my terrible quality pictures.
3.
What is the fundamental period of the following equation.
$ y(t)=4sin(3t+pi/6) $
Its fundamental period is $ = 2pi/3 $
Comments and Questions...