Periodic Functions in Continuous Time
- Functions are classified as periodic if there exists $ T>0\! $ such that $ y(x+T)=y(x)\! $.
The following is an example of a periodic function:
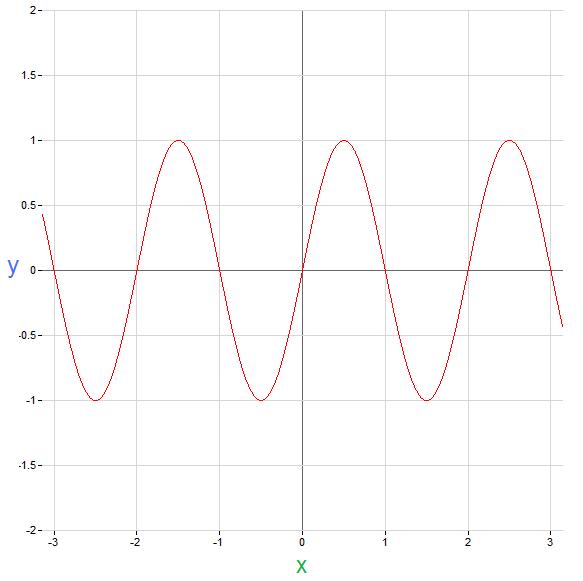
This function is periodic because $ y(x)=y(x+T)\! $ for $ T=0, 2, 4, 6\! $ etc.
Non-Periodic Functions in Continuous Time
- Functions are classified as non-periodic if there exists no $ T>0\! $ such that $ y(x+T)=y(x)\! $.
The following is an example of a non-periodic function:

This function is not periodic because there exists no T where $ y(x)=y(x+T)\! $.

