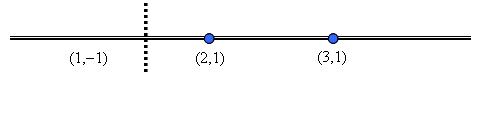
The class of the data is written as the second co-ordinate.
$ {\alpha }_{1}+{\alpha }_{2}+{\alpha }_{3}=0 $
- 3 inequalities**:
$ 1.w+b\leq-1 $
$ 2.w+b\leq+1 $
$ 3.w+b\leq+1 $
$ J=\frac{{w}^{2}}{2}-{\alpha }_{1}\left(-w-b-1 \right)-{\alpha }_{2}(2w+b-1)-{\alpha }_{3}(3w+b-1) $
Formulating the Dual Problem:
$ Q(\alpha )= {\alpha }_{1}+{\alpha }_{2}+{\alpha }_{3}-[0.5{{\alpha }_{1}}^{2}+2{{\alpha }_{2}}^{2}+4.5{{\alpha }_{3}}^{2}-2{\alpha }_{1}{\alpha }_{2}-3{\alpha }_{1}{\alpha }_{3}-6{\alpha }_{2}{\alpha }_{3}] $
Subject to constraints
$ {\alpha }_{1}+{\alpha }_{2}+{\alpha }_{3}=0 $ and
$ {\alpha }_{1}\geq 0; {\alpha }_{2}\geq 0;{\alpha }_{3}\geq 0 $
Differentiating partially with respect to $ {\alpha }_{1},{\alpha }_{2}, {\alpha }_{3} $
$ {\alpha }_{1}+2{\alpha }_{2}+3{\alpha }_{3}=0 $
$ 1+2{\alpha }_{1}-4{\alpha }_{2}-6{\alpha }_{3}=0 $
$ 1+3{\alpha }_{1}-6{\alpha }_{2}-9{\alpha }_{3}=0 $
On Solving, we get
$ {\alpha }_{1}=2 $
$ {\alpha }_{2}=2 $
$ {\alpha }_{3}=0 $
This yields w = 2, b = -3. Hence the solution of decision boundary is: 2x - 3 = 0. or x = 1.5 This is shown as the dash line in above figure.
