Part A: Periodic Signals Revisited...Periodic Signals Revisited...Periodic Signals Revisited
As we discussed in class, a function $ x(t) $ is periodic if $ x(t+T)= x(t) $ , where T is a multiple of the fundamental period, or smallest period.
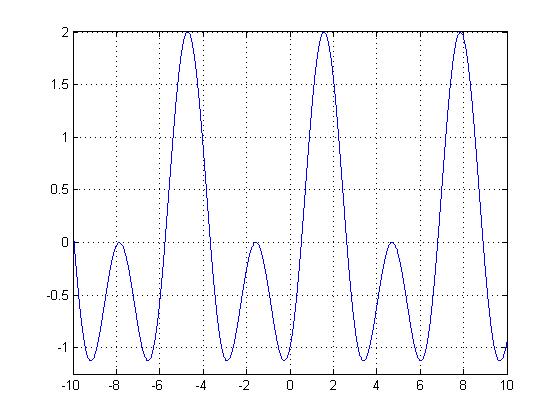
In the first homework, I explained how $ sin(t) $ was periodic. However, because that is rather boring, let's take a look at $ sin(t)-cos(2t) $.
Note how much more exciting $ sin(t)-cos(2t) $ is than $ sin(t) $. Here the sampling frequency is very small, on the order of $ 10^4 $