(Created page with "Category:Walther MA271 Fall2020 topic2 =Restrictions of Stationary Distribution In the last section, it is emphasized that steady-state vectors can be derived only with...") |
|||
| Line 8: | Line 8: | ||
<center>[[File:Statediagram.jpg|500px|thumbnail]]</center> | <center>[[File:Statediagram.jpg|500px|thumbnail]]</center> | ||
| + | |||
| + | We can also write that in matrix form: | ||
<center>[[File:Transitionmatrix2.jpg|500px|thumbnail]]</center> | <center>[[File:Transitionmatrix2.jpg|500px|thumbnail]]</center> | ||
| + | |||
| + | Going back to the Python program from before, when the initial state is <math>[1, 0, 0]</math>, | ||
| + | |||
| + | <center>[[File:Pythondemo7.jpg|500px|thumbnail]]</center> | ||
| + | |||
| + | <center>[[File:Pythondemo8.jpg|500px|thumbnail]]</center> | ||
[[ Walther MA271 Fall2020 topic2|Back to Markov Chains]] | [[ Walther MA271 Fall2020 topic2|Back to Markov Chains]] | ||
[[Category:MA271Fall2020Walther]] | [[Category:MA271Fall2020Walther]] | ||
Revision as of 03:35, 6 December 2020
=Restrictions of Stationary Distribution
In the last section, it is emphasized that steady-state vectors can be derived only with regular matrices. What if these vectors are not regular?
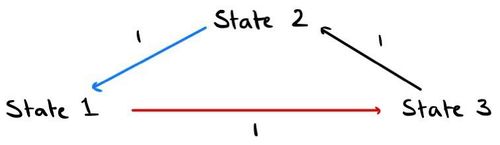
Consider a periodic Markov chain:
We can also write that in matrix form:
Going back to the Python program from before, when the initial state is $ [1, 0, 0] $,
File:Pythondemo7.jpg
500px
File:Pythondemo8.jpg
500px