(→Example of a Linear System) |
(→Linear Systems) |
||
| Line 2: | Line 2: | ||
Because we are engineers we will use a picture to describe a linear system: | Because we are engineers we will use a picture to describe a linear system: | ||
| − | [[Image: | + | [[Image:Systempjcannon3_ECE301Fall2008mboutin.JPG]] |
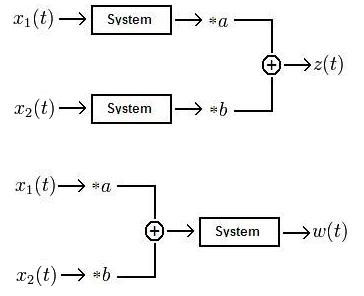
Where <math>a \!</math> and <math>b\!</math> are real or complex. The system is defined as linear if <math>z(t)=w(t)\!</math> | Where <math>a \!</math> and <math>b\!</math> are real or complex. The system is defined as linear if <math>z(t)=w(t)\!</math> | ||
Revision as of 12:33, 11 September 2008
Linear Systems
Because we are engineers we will use a picture to describe a linear system:
Where $ a \! $ and $ b\! $ are real or complex. The system is defined as linear if $ z(t)=w(t)\! $
In other words, if in one scenario we have two signals put into a system, multiplied by a variable, then summed together, the output should equal the output of a second scenario where the signals are multiplied by a variable, summed together, then put through the same system. If this is true, then the system is defined as linear.
Example of a Linear System
Let $ y(t)=x(t) \! $. Then:
$ y_1(t)=x_1(t) y_2(t)=x_2(t) ax_1(t) bx_2(t) ax_1(t)+bx_2(t) \! $