| Line 77: | Line 77: | ||
</math> | </math> | ||
| − | [[Image:MN081.png|Alt text| | + | [[Image:MN081.png|Alt text|500x500px]] |
<math> | <math> | ||
| Line 89: | Line 89: | ||
at $\tau_1; V$ goes to 0. Then this process repeats in the next 2 cycles. | at $\tau_1; V$ goes to 0. Then this process repeats in the next 2 cycles. | ||
| − | [[Image:MN082.png|Alt text| | + | [[Image:MN082.png|Alt text|500x500px]] |
<math> | <math> | ||
Revision as of 10:57, 6 August 2017
MICROELECTRONICS and NANOTECHNOLOGY (MN)
Question 1: Semiconductor Fundamentals
August 2008
Questions
All questions are in this link
Solutions of all questions
a)
$ \begin{align*} \frac{1}{m^*} &= \frac{1}{\hslash^2}\frac{d^2E}{dk^2} \\ &=\frac{1}{\hslash^2}\frac{d^2}{dk^2}(\alpha k^2) \\ &=2\alpha/\hslash^2 \\ \therefore m^* &= \frac{\hslash^2}{2\alpha} \end{align*} $
------------------------------------------------------------------------------------ b)
$ \begin{align*} g(E) &=\frac{\pi(k+\triangle k)^2 - \pi k^2}{\frac{2\pi}{W}\cdot\frac{2\pi}{L}}\cdot\frac{1}{\triangle E}\cdot\frac{1}{WL}\\ &\approx \frac{1}{4\pi^2}\cdot(\pi\cdot2k\triangle k)\cdot\frac{1}{\triangle E}\\ &=\frac{1}{2\pi}k\frac{\triangle k}{\triangle E}\approx = \frac{1}{2\pi}k\frac{dk}{dE} \end{align*} $
$ k = \bigg(E/\alpha\bigg)^{\frac{1}{2}} $
$ \therefore \frac{dk}{dE} = \frac{1}{2}\frac{E^{-\frac{1}{2}}}{\alpha^{-\frac{1}{2}}}\cdot\frac{1}{\alpha} = \frac{\alpha^{-\frac{1}{2}}}{2}E^{-\frac{1}{2}} $
$ \begin{align*} \therefore g(E) &= \frac{1}{2\pi}\cdot\frac{E^{\frac{1}{2}}}{\alpha^{\frac{1}{2}}}\cdot\frac{\alpha^{-\frac{1}{2}}}{2}E^{-\frac{1}{2}}\\ &=\frac{1}{4\pi \alpha} \end{align*} $
-------------------------------------------------------------------------------------- c)
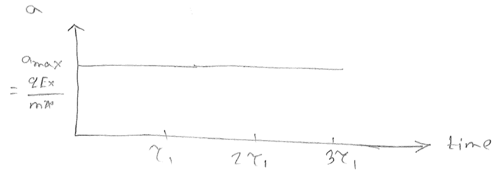
$ \begin{align*} F&=-qE=qE_x\:\:\:\:\:\:\:\:\:\:\text{(+x direction)}\\ F &=m^*a = qE_x\\ \therefore a_{max} &=\frac{qE_x}{m^*}=a \:\:\:\:\:\:\:\:\:\:\text{(constant)} \end{align*} $
$ V(t) = \int_0^t a dt =at=\frac{qE_xt}{m^*} $
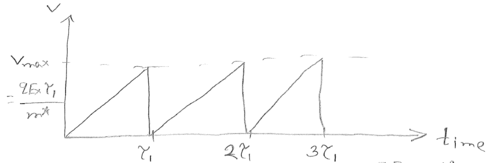
$ V_{max} = V(\tau_1) = a\tau_1=\frac{qE_x\tau_1}{m^*} $
at $\tau_1; V$ goes to 0. Then this process repeats in the next 2 cycles.
$ x(t) = \int_0^tVdt=\int_0^t\frac{qE_x}{m^*}tdt = \frac{qE_x}{m^*}\cdot\frac{t^2}{2} $
$ \therefore x(\tau_1) =\frac{qE_x}{m^*}\cdot\frac{\tau_1^2}{2} $
At $ t = \tau_1 $; electron will be at $ x(\tau_1). $ For the next cycle; this position will be the initial one.
--------------------------------------------------------------------------------------
d)
$ v_{avg} = \mu E \text{ (So, we use the $2^{nd}$ plot)} $
$ \therefore \mu = \frac{v_{avg}}{E} $
So, we need to find avg. velocity and divide by the constant electric field value to find mobility.
$ v_{avg} = \frac{V(0)+V(\tau_1)}{2} = \frac{V(\tau_1)}{2} = \frac{qE_x\tau_1}{2m^*} $
$ \therefore \mu = \frac{qE_x\tau_1}{2m^*E_x} = \frac{q\tau_1}{2m^*}. $
-------------------------------------------------------------------------------------- e) For elastic scattering, velocity cannot change. As the velocity goes to zero here, it cannot be elastic.\\ Ans: ii