| Line 1: | Line 1: | ||
| − | MA 279 | + | MA 279<br /> |
| − | Christine Zhang | + | Christine Zhang<br /> |
| − | Jennifer Nance | + | Jennifer Nance<br /> |
| − | Abhijeet Gaurav | + | Abhijeet Gaurav<br /> |
| − | Evgenii Grunin | + | Evgenii Grunin<br /> |
| − | Instructor: Uli Walther | + | Instructor: Uli Walther<br /> |
| + | == Dijkstra’s Algorithm and Its Variants for Shortest Path == | ||
| + | '''Introduction'''<br /> | ||
| + | Dijkstra algorithm belongs to a family of Best First Search algorithms, and therefore used to find the shortest path between two points on a graph. Finding such path in a graph may serve as an abstraction for solving real world problems such as finding shortest route in road networks. The points or vertices in the graph may represent cities and the edges may represent roads connecting the cities. Each edge in Dijkstra algorithm is assigned a number, which represents distance of each route. Common services such as MapQuest can use this algorithm to find the shortest route between two points on a map. In a separate approach, network routing, the algorithm can be used to find the shortest path for data packets to take in a switching network. Another common use of Dijkstra algorithm and its variants can be found in the fields of Telephone and Flight networks.<br />The algorithm that determines shortest paths from a source point or common vertex to all other points or vertices was introduced by the Dutch computer scientist, Edsger W. Dijkstra. His work was discovered in 1956 and published in 1959. This three-page publication was titled: “A note on two problems in connexion with graphs”. Dijkstra first came up with the idea when working at the Mathematical Center in Amsterdam. As a programmer, he wanted to find a way to demonstrate capabilities of computer called ‘ARMAC’. His first shortest path problem was implemented for a simplified transportation map for 64 cities of the Netherlands. | ||
| − | + | '''Algorithm'''<br /> | |
| − | + | An algorithm runs on a weighted graph that starts with an initial node and a goal destination node and then finds the least cost path to the goal node. Assign to every node a tentative distance value so the first node is set to zero and all the other nodes are set to infinity. Starting at the initial node we consider all if its unvisited neighbors and calculate the distance to the current node plus the distance from the current node to the neighbor node. If this value is less than the current tentative distance of the specified node, then we replace it with its new value. <br /> | |
| − | + | (node X tentative distance value) = (tentative distance for current node) + (Distance from current node to Neighbor node X)<br /> | |
| − | + | Node tentative distance value X = Min { node X tentative distance value calculated , Tentative distance value already labeled on the node X}<br /> | |
| − | + | After all neighbours of the current node have been evaluated, we update shortest distances reached so far, mark the current node as visited (or add it to the visited list) and remove it from the unvisited list. Set the unvisited node marked with the smallest tentative distance as the next current node and then The algorithm then iterates until the destination vertex is reached or no further improvement can be made (case when source and destination vertices are disconnected).<br /> | |
| − | '''Algorithm''' | + | This algorithm only calculates the shortest path from point A to point B. All nodes do not have to be included in the path from point A to point B, all nodes don’t have to be explored and may have a tentative distance of infinity at the conclusion of the algorithm. <br /> |
| − | An algorithm runs on a weighted graph that starts with an initial node and a goal destination node and then finds the least cost path to the goal node. Assign to every node a tentative distance value so the first node is set to zero and all the other nodes are set to infinity. Starting at the initial node we consider all if its unvisited neighbors and calculate the distance to the current node plus the distance from the current node to the neighbor node. If this value is less than the current tentative distance of the specified node, then we replace it with its new value. | + | Here is sample pseudocode for Dijkstra's algorithm implementation:<br /> |
| − | (node X tentative distance value) = (tentative distance for current node) + (Distance from current node to Neighbor node X) | + | |
| − | Node tentative distance value X = Min { node X tentative distance value calculated , Tentative distance value already labeled on the node X} | + | |
| − | After all neighbours of the current node have been evaluated, we update shortest distances reached so far, mark the current node as visited (or add it to the visited list) and remove it from the unvisited list. Set the unvisited node marked with the smallest tentative distance as the next current node and then The algorithm then iterates until the destination vertex is reached or no further improvement can be made (case when source and destination vertices are disconnected). | + | |
| − | This algorithm only calculates the shortest path from point A to point B. All nodes do not have to be included in the path from point A to point B, all nodes don’t have to be explored and may have a tentative distance of infinity at the conclusion of the algorithm. | + | |
| − | Here is sample pseudocode for Dijkstra's algorithm implementation: | + | |
'''Dijkstra’s Algorithm:''' | '''Dijkstra’s Algorithm:''' | ||
| − | s – starting node | + | s – starting node<br /> |
| − | DT – Distance Table, | + | DT – Distance Table,<br /> |
| − | PQ – priority queue, the priority of a node is equal to the distance from s to that node | + | PQ – priority queue, the priority of a node is equal to the distance from s to that node<br /> |
| − | Initialize DT(s,0) = 0, DT(s,1) = 0, all remaining DT(j,k) = -1 | + | Initialize DT(s,0) = 0, DT(s,1) = 0, all remaining DT(j,k) = -1<br /> |
| − | Store s in PQ with distance = 0 | + | Store s in PQ with distance = 0<br /> |
| − | While there are vertices in the queue: | + | While there are vertices in the queue:<br /> |
| − | DeleteMin a vertex v from the queue | + | DeleteMin a vertex v from the queue<br /> |
| − | For all adjacent vertices w: | + | For all adjacent vertices w:<br /> |
| − | Compute new_distance = (distance to v) + (distance(v,w)) | + | Compute new_distance = (distance to v) + (distance(v,w))<br /> |
| − | i.e. new_distance = DT(v,0) + distance(v,w) | + | i.e. new_distance = DT(v,0) + distance(v,w)<br /> |
| − | If distance to w not computed (DT(w,0) = -1) | + | If distance to w not computed (DT(w,0) = -1) <br /> |
| − | store new distance in table : DT(w,0)= new_distance | + | store new distance in table : DT(w,0)= new_distance<br /> |
| − | append w in PQ with priority new_distance | + | append w in PQ with priority new_distance<br /> |
| − | make path to w equal to v, i.e. DT(w,1) = v | + | make path to w equal to v, i.e. DT(w,1) = v<br /> |
| − | else | + | else<br /> |
| − | if old distance > new distance, i.e. DT(w,0) > new_distance | + | if old distance > new distance, i.e. DT(w,0) > new_distance<br /> |
| − | Update old_distance = new_distance, i.e. DT(w,0) = new_distance | + | Update old_distance = new_distance, i.e. DT(w,0) = new_distance<br /> |
| − | Update the priority of w in PQ | + | Update the priority of w in PQ <br /> |
| − | (this is done by updating the priority of an element in the queue -decreaseKey operation. Complexity O(logV)) | + | (this is done by updating the priority of an element in the queue -decreaseKey operation. Complexity O(logV)) <br /> |
| − | Update path to w to be v, i.e. DT(w,1) = v | + | Update path to w to be v, i.e. DT(w,1) = v<br /> |
| − | + | <br /> | |
| − | '''Example''' | + | '''Example'''<br /> |
[[File:Work.jpg|thumbnail|Figure 1A]] | [[File:Work.jpg|thumbnail|Figure 1A]] | ||
| − | + | <br /> | |
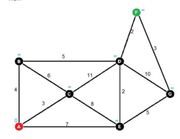
| − | In Figure 1A, A is the initial node and F is the goal destination node. The initial node starts with a tentative distance value of 0 while all other nodes start with infinity. To start we look at all neighboring nodes from A which are B,C and E. We then calculate the tentative distance for each of these nodes, B is the min (∞, 0+4) = 4; C is the min(∞,0+3)=3, E is the min ( ∞, 0+7) = 7. Out of all the neighboring nodes, C has the shortest distance, so C becomes the current node and we add C to the visited list. Then the process repeats. We look at the neighboring nodes of C which are B, D and E. B is the min ( 4, 6+3) = 4; D is min (∞, 3+11)=14; E is min(7, 3+8) = 7. In this round B has the smallest tentative distance so we visit B who only has neighbor of D since C has been visited. D is the min ( 14, 4+5 ) = 9 but E has not been visited and has a weight of 7 which is less than 9, so we visit node E. E as the current node, D and G have not been visited, so D is the min ( 9, 2+7)=9; G is the min(∞,7+5)=12. Therefore, we visit D which was calculated from A to B to D . Then, lastly F is the min ( ∞, 9+2)=11 so we visit F because G has a value of 12. Therefore, the path is from A to B to D to F. | + | In Figure 1A, A is the initial node and F is the goal destination node. The initial node starts with a tentative distance value of 0 while all other nodes start with infinity. To start we look at all neighboring nodes from A which are B,C and E. We then calculate the tentative distance for each of these nodes, B is the min (∞, 0+4) = 4; C is the min(∞,0+3)=3, E is the min ( ∞, 0+7) = 7. Out of all the neighboring nodes, C has the shortest distance, so C becomes the current node and we add C to the visited list. Then the process repeats. We look at the neighboring nodes of C which are B, D and E. B is the min ( 4, 6+3) = 4; D is min (∞, 3+11)=14; E is min(7, 3+8) = 7. In this round B has the smallest tentative distance so we visit B who only has neighbor of D since C has been visited. D is the min ( 14, 4+5 ) = 9 but E has not been visited and has a weight of 7 which is less than 9, so we visit node E. E as the current node, D and G have not been visited, so D is the min ( 9, 2+7)=9; G is the min(∞,7+5)=12. Therefore, we visit D which was calculated from A to B to D . Then, lastly F is the min ( ∞, 9+2)=11 so we visit F because G has a value of 12. Therefore, the path is from A to B to D to F. <br /> |
| − | Dijkstra’s algorithm fails to work if it encounters negative cycles or negative edges. | + | Dijkstra’s algorithm fails to work if it encounters negative cycles or negative edges.However, this problem can be solved using Bellman-Ford algorithm.<br /> |
| − | However, this problem can be solved using Bellman-Ford algorithm. | + | Example when Dijkstra’s algorithm (with min-heap priority queue) fails:<br /> |
| − | Example when Dijkstra’s algorithm (with min-heap priority queue) fails: | + | |
[[File:Notwork1.jpg|thumbnail|Figure 1B]] | [[File:Notwork1.jpg|thumbnail|Figure 1B]] | ||
| − | + | <br /> | |
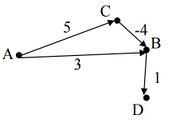
| − | Firstly in Figure 1B, the source vertex A is popped out of the queue and edges (A, C) and (A, B) are relaxed. | + | Firstly in Figure 1B, the source vertex A is popped out of the queue and edges (A, C) and (A, B) are relaxed.<br /> |
[[File:Notwork2.jpg|thumbnail|Figure 2B]] | [[File:Notwork2.jpg|thumbnail|Figure 2B]] | ||
| − | + | <br /> | |
| − | + | Secondly in Figure 2B, we have B on the top of our min-heap. Our algorithm now pops B and relaxes the only edge out of B i.e. (B, D) and thus we get distance of D = 3 + 1 = 4.<br /> | |
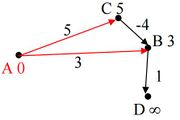
| − | Secondly in Figure 2B, we have B on the top of our min-heap. Our algorithm now pops B and relaxes the only edge out of B i.e. (B, D) and thus we get distance of D = 3 + 1 = 4. | + | |
[[File:Notwork3.jpg|thumbnail|Figure 3B]] | [[File:Notwork3.jpg|thumbnail|Figure 3B]] | ||
| − | + | <br /> | |
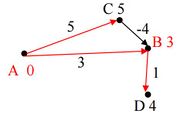
| − | + | Now, we have vertex D, shown in Figure 3B on the top of the min-heap and we remove vertex D. Also, we don’t have any edges going out of D to relax. The only vertex left in the queue is C. We now remove C and relax the edge (C, B). Since, we have 5 - 4 = 1 < 3, distance to B must be updated to 1.<br /> | |
| − | Now, we have vertex D, shown in Figure 3B on the top of the min-heap and we remove vertex D. Also, we don’t have any edges going out of D to relax. The only vertex left in the queue is C. We now remove C and relax the edge (C, B). Since, we have 5 - 4 = 1 < 3, distance to B must be updated to 1. | + | |
[[File:Notwork4.jpg|thumbnail|Figure 4B]] | [[File:Notwork4.jpg|thumbnail|Figure 4B]] | ||
| − | + | <br /> | |
| − | The algorithm will now terminate because our queue has become empty. However, our path from A -> C -> B -> D has a total length of 5 + (-4) + 1 = 2 < 4 as shown in Figure 4B. Therefore, clearly Dijkstra’s algorithm fails to correctly evaluate shortest path from A to D. | + | The algorithm will now terminate because our queue has become empty. However, our path from A -> C -> B -> D has a total length of 5 + (-4) + 1 = 2 < 4 as shown in Figure 4B. Therefore, clearly Dijkstra’s algorithm fails to correctly evaluate shortest path from A to D.<br /> |
| − | Variations | + | '''Variations'''<br /> |
| − | In some sense Dijkstra may be viewed as one of the most fundamental algorithms for solving the shortest path problem. There are numerous variants and extensions of Dijkstra algorithm; moreover, Dijkstra can be also often modified to solve various problem-specific tasks, therefore, we will concentrate only on one of the most famous variants of Dijkstra. In general, there are 3 main aspects of Dijkstra algorithms that can be modified or extended: Distance (distance meaning and evaluation between vertices and from a given vertex to final destination), underlying Data Structure (binary heap priority queue, for example, may be slightly modified or substituted completely with another data structure like list), and finally Relaxation and Distance Initialization (method of evaluating the opportunity of possible path improvement and method of initializing all distances between vertices respectively). | + | In some sense Dijkstra may be viewed as one of the most fundamental algorithms for solving the shortest path problem. There are numerous variants and extensions of Dijkstra algorithm; moreover, Dijkstra can be also often modified to solve various problem-specific tasks, therefore, we will concentrate only on one of the most famous variants of Dijkstra. In general, there are 3 main aspects of Dijkstra algorithms that can be modified or extended: Distance (distance meaning and evaluation between vertices and from a given vertex to final destination), underlying Data Structure (binary heap priority queue, for example, may be slightly modified or substituted completely with another data structure like list), and finally Relaxation and Distance Initialization (method of evaluating the opportunity of possible path improvement and method of initializing all distances between vertices respectively).<br /> |
| − | As we mentioned, some different types of modification are dependent on the problem to be solved, so for simplicity we will use a problem of finding shortest path between cities (represented by vertices) as an example, since it is most common and intuitive to understand. | + | As we mentioned, some different types of modification are dependent on the problem to be solved, so for simplicity we will use a problem of finding shortest path between cities (represented by vertices) as an example, since it is most common and intuitive to understand.<br /> |
| − | One of the most common modifications of Dijkstra is the Greedy Best First Search approach. Such an algorithm is driven by exactly same idea as Dijkstra (or in some sense Dijkstra, being part of BFS algorithms family, can be seen as a modification of Greedy Best First Search, but this is not the topic of our discussion), but instead of using the actual distances between vertices, it uses a so-called heuristic function that abstracts these distances. The choice of a heuristic function may vary and again is dependent on the type of a problem, but one possibility is to use shortest distances (think in terms of planar geometry, not in terms of actuals roads) from a city to a final destination. In Figure 5 the actual roads are bold lines, so using the described heuristic the distance from A (assuming B is the destination vertex) would be the length of straight (dashed) line between A and B: | + | One of the most common modifications of Dijkstra is the Greedy Best First Search approach. Such an algorithm is driven by exactly same idea as Dijkstra (or in some sense Dijkstra, being part of BFS algorithms family, can be seen as a modification of Greedy Best First Search, but this is not the topic of our discussion), but instead of using the actual distances between vertices, it uses a so-called heuristic function that abstracts these distances. The choice of a heuristic function may vary and again is dependent on the type of a problem, but one possibility is to use shortest distances (think in terms of planar geometry, not in terms of actuals roads) from a city to a final destination. In Figure 5 the actual roads are bold lines, so using the described heuristic the distance from A (assuming B is the destination vertex) would be the length of straight (dashed) line between A and B:<br /> |
[[File:Var.jpg|thumbnail|Figure 5]] | [[File:Var.jpg|thumbnail|Figure 5]] | ||
| − | + | <br /> | |
| − | Such algorithm offers an ease of computation and sometimes yields better (faster search) performance, however, as most of the algorithms that are based entirely on heuristics, does not guarantee to find the best (the shortest path) solution or even reach the final destination. | + | Such algorithm offers an ease of computation and sometimes yields better (faster search) performance, however, as most of the algorithms that are based entirely on heuristics, does not guarantee to find the best (the shortest path) solution or even reach the final destination.<br /> |
| − | The next common extension of Dijkstra is A* algorithm, which is very similar to Greedy Best First Search, but uses both heuristic function and the actual distances between vertices. A* is considered to be one of the most popular and powerful short path algorithms and is often preferred to Dijkstra, as its use of heuristics can significantly increase the performance. | + | The next common extension of Dijkstra is A* algorithm, which is very similar to Greedy Best First Search, but uses both heuristic function and the actual distances between vertices. A* is considered to be one of the most popular and powerful short path algorithms and is often preferred to Dijkstra, as its use of heuristics can significantly increase the performance.<br /> |
| − | The next well-known algorithm that relies on the Dijkstra algorithm is Johnson's algorithm. Johnson's algorithm uses Bellman-Ford algorithm to deal with negative weights and transform the input graph into one that can be processed by Dijkstra algorithm. Johnson's implementation also uses Fibonacci-heap min priority queue instead of a Binary Heap, which yields not only exposure to a larger set of problems, but also a better performance. | + | The next well-known algorithm that relies on the Dijkstra algorithm is Johnson's algorithm. Johnson's algorithm uses Bellman-Ford algorithm to deal with negative weights and transform the input graph into one that can be processed by Dijkstra algorithm. Johnson's implementation also uses Fibonacci-heap min priority queue instead of a Binary Heap, which yields not only exposure to a larger set of problems, but also a better performance.<br /> |
| − | As mentioned earlier the most common implementation of Dijkstra algorithm uses binary heap as its underlying data structure. There are, however, numerous modifications that could be made to the data structure in order to increase the performance or satisfy a particular goal. The most popular modifications include Dijkstra algorithm with Fibonacci heap, list, indexed priority queue, D-way heap and array. We compare run time complexity later in the discussion, but in general an array implementation is often used when dealing with dense graphs, while binary heap is significantly better performance-wise with sparse graphs. D-way head reduces computational cost compared to a binary heap, while Fibonacci heap, being extremely difficult in implementation, theoretically yields one of the best performances amongst all other Dijkstra modifications. | + | As mentioned earlier the most common implementation of Dijkstra algorithm uses binary heap as its underlying data structure. There are, however, numerous modifications that could be made to the data structure in order to increase the performance or satisfy a particular goal. The most popular modifications include Dijkstra algorithm with Fibonacci heap, list, indexed priority queue, D-way heap and array. We compare run time complexity later in the discussion, but in general an array implementation is often used when dealing with dense graphs, while binary heap is significantly better performance-wise with sparse graphs. D-way head reduces computational cost compared to a binary heap, while Fibonacci heap, being extremely difficult in implementation, theoretically yields one of the best performances amongst all other Dijkstra modifications. <br /> |
| − | '''Time Complexity Analysis''' | + | '''Time Complexity Analysis'''<br /> |
The most commonly used Dijkstra’s algorithm uses binary heap. However, the running time complexity of variants/modification of Dijkstra’s algorithm depends on the way it is implemented. The Dijkstra’s algorithm can be implemented more efficiently if we store the graph in the form of adjacency list and using balancing binary search tree/ binary heap/ pairing heap/ fibonacci heap as our priority queue to implement extracting minimum efficiently. | The most commonly used Dijkstra’s algorithm uses binary heap. However, the running time complexity of variants/modification of Dijkstra’s algorithm depends on the way it is implemented. The Dijkstra’s algorithm can be implemented more efficiently if we store the graph in the form of adjacency list and using balancing binary search tree/ binary heap/ pairing heap/ fibonacci heap as our priority queue to implement extracting minimum efficiently. | ||
| − | Since, the algorithm fundamentally depends on time complexity of Extract-Min and Decrease-Key operation described in the pseudocode earlier, the time complexity of the Dijkstra’s algorithm can be generally be given by: | + | Since, the algorithm fundamentally depends on time complexity of Extract-Min and Decrease-Key operation described in the pseudocode earlier, the time complexity of the Dijkstra’s algorithm can be generally be given by:<br /> |
| − | Θ (V) Textract-min + Θ (E) Tdecrease-key | + | Θ (V) Textract-min + Θ (E) Tdecrease-key<br /> |
| − | Therefore, if we use a simple linked list or array to store the vertex set, and if our extract-minimum operation is a simple linear search through all the vertices, the running time is O (E + V ^2) = O (V^2). | + | Therefore, if we use a simple linked list or array to store the vertex set, and if our extract-minimum operation is a simple linear search through all the vertices, the running time is O (E + V ^2) = O (V^2).<br /> |
| − | The most commonly implemented Dijkstra’s algorithm uses a binary heap priority queue, the complexity of this algorithm is O (E logV + V logV) = O ((E + V)log(V)) = O (ElogV) because V is O (E). | + | The most commonly implemented Dijkstra’s algorithm uses a binary heap priority queue, the complexity of this algorithm is O (E logV + V logV) = O ((E + V)log(V)) = O (ElogV) because V is O (E).<br /> |
| − | Finally, if we use a more complicated priority queue called Fibonacci Heap, the asymptotic complexity of Dijkstra’s algorithm reduces to O (E + V log V). | + | Finally, if we use a more complicated priority queue called Fibonacci Heap, the asymptotic complexity of Dijkstra’s algorithm reduces to O (E + V log V). <br /> |
| − | There is a an specialized variant of Dijkstra’s algorithm which uses a special priority queue structure by Van Emde Boas in which edge weights are integers bounded by some constant C. This variant brings the complexity down to O (E log log |C|). Also, there is an another implementation of Dijkstra’s algorithm which uses a combination of radix heap and fibonacci heap. The running time of this implementation is O (E + V (log C)^0.5). | + | There is a an specialized variant of Dijkstra’s algorithm which uses a special priority queue structure by Van Emde Boas in which edge weights are integers bounded by some constant C. This variant brings the complexity down to O (E log log |C|). Also, there is an another implementation of Dijkstra’s algorithm which uses a combination of radix heap and fibonacci heap. The running time of this implementation is O (E + V (log C)^0.5).<br /> |
| − | + | The running time complexity of Bellman-Ford algorithm which works with negative edges (and Dijkstra’s algorithm fails) is O (E V).<br /> | |
| − | We have briefly covered one of the most famous and influential variants and extensions of Dijkstra algorithm, but it can be clearly seen that many more exist and could be created in order to satisfy particular needs of a developer. | + | We have briefly covered one of the most famous and influential variants and extensions of Dijkstra algorithm, but it can be clearly seen that many more exist and could be created in order to satisfy particular needs of a developer.<br /> |
| − | References: | + | References:<br /> |
| − | http://www.cse.unsw.edu.au/~cs2011/05s2/assignment4-solutions.pdf | + | http://www.cse.unsw.edu.au/~cs2011/05s2/assignment4-solutions.pdf<br /> |
| − | http://faculty.simpson.edu/lydia.sinapova/www/cmsc250/LN250_Weiss/L27-GraphSummary.htm | + | http://faculty.simpson.edu/lydia.sinapova/www/cmsc250/LN250_Weiss/L27-GraphSummary.htm<br /> |
https://en.wikipedia.org/wiki/Shortest_path_problem | https://en.wikipedia.org/wiki/Shortest_path_problem | ||
| − | + | <br /> | |
http://www.csl.mtu.edu/cs2321/www/newLectures/30_More_Dijkstra.htm | http://www.csl.mtu.edu/cs2321/www/newLectures/30_More_Dijkstra.htm | ||
| − | + | <br /> | |
https://www.cs.princeton.edu/~rs/AlgsDS07/15ShortestPaths.pdf | https://www.cs.princeton.edu/~rs/AlgsDS07/15ShortestPaths.pdf | ||
| − | + | <br /> | |
https://www.youtube.com/watch?v=gdmfOwyQlcI | https://www.youtube.com/watch?v=gdmfOwyQlcI | ||
| − | + | <br /> | |
https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm | https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm | ||
| − | + | <br /> | |
https://en.wikipedia.org/wiki/Edsger_W._Dijkstra#Algorithmic_work | https://en.wikipedia.org/wiki/Edsger_W._Dijkstra#Algorithmic_work | ||
| − | + | <br /> | |
http://www.codeproject.com/Articles/19919/Shortest-Path-Problem-Dijkstra-s-Algorithm | http://www.codeproject.com/Articles/19919/Shortest-Path-Problem-Dijkstra-s-Algorithm | ||
| − | + | <br /> | |
[[Category:MA279Spring2016Walther]] | [[Category:MA279Spring2016Walther]] | ||
Revision as of 23:11, 24 April 2016
MA 279
Christine Zhang
Jennifer Nance
Abhijeet Gaurav
Evgenii Grunin
Instructor: Uli Walther
Dijkstra’s Algorithm and Its Variants for Shortest Path
Introduction
Dijkstra algorithm belongs to a family of Best First Search algorithms, and therefore used to find the shortest path between two points on a graph. Finding such path in a graph may serve as an abstraction for solving real world problems such as finding shortest route in road networks. The points or vertices in the graph may represent cities and the edges may represent roads connecting the cities. Each edge in Dijkstra algorithm is assigned a number, which represents distance of each route. Common services such as MapQuest can use this algorithm to find the shortest route between two points on a map. In a separate approach, network routing, the algorithm can be used to find the shortest path for data packets to take in a switching network. Another common use of Dijkstra algorithm and its variants can be found in the fields of Telephone and Flight networks.
The algorithm that determines shortest paths from a source point or common vertex to all other points or vertices was introduced by the Dutch computer scientist, Edsger W. Dijkstra. His work was discovered in 1956 and published in 1959. This three-page publication was titled: “A note on two problems in connexion with graphs”. Dijkstra first came up with the idea when working at the Mathematical Center in Amsterdam. As a programmer, he wanted to find a way to demonstrate capabilities of computer called ‘ARMAC’. His first shortest path problem was implemented for a simplified transportation map for 64 cities of the Netherlands.
Algorithm
An algorithm runs on a weighted graph that starts with an initial node and a goal destination node and then finds the least cost path to the goal node. Assign to every node a tentative distance value so the first node is set to zero and all the other nodes are set to infinity. Starting at the initial node we consider all if its unvisited neighbors and calculate the distance to the current node plus the distance from the current node to the neighbor node. If this value is less than the current tentative distance of the specified node, then we replace it with its new value.
(node X tentative distance value) = (tentative distance for current node) + (Distance from current node to Neighbor node X)
Node tentative distance value X = Min { node X tentative distance value calculated , Tentative distance value already labeled on the node X}
After all neighbours of the current node have been evaluated, we update shortest distances reached so far, mark the current node as visited (or add it to the visited list) and remove it from the unvisited list. Set the unvisited node marked with the smallest tentative distance as the next current node and then The algorithm then iterates until the destination vertex is reached or no further improvement can be made (case when source and destination vertices are disconnected).
This algorithm only calculates the shortest path from point A to point B. All nodes do not have to be included in the path from point A to point B, all nodes don’t have to be explored and may have a tentative distance of infinity at the conclusion of the algorithm.
Here is sample pseudocode for Dijkstra's algorithm implementation:
Dijkstra’s Algorithm:
s – starting node
DT – Distance Table,
PQ – priority queue, the priority of a node is equal to the distance from s to that node
Initialize DT(s,0) = 0, DT(s,1) = 0, all remaining DT(j,k) = -1
Store s in PQ with distance = 0
While there are vertices in the queue:
DeleteMin a vertex v from the queue
For all adjacent vertices w:
Compute new_distance = (distance to v) + (distance(v,w))
i.e. new_distance = DT(v,0) + distance(v,w)
If distance to w not computed (DT(w,0) = -1)
store new distance in table : DT(w,0)= new_distance
append w in PQ with priority new_distance
make path to w equal to v, i.e. DT(w,1) = v
else
if old distance > new distance, i.e. DT(w,0) > new_distance
Update old_distance = new_distance, i.e. DT(w,0) = new_distance
Update the priority of w in PQ
(this is done by updating the priority of an element in the queue -decreaseKey operation. Complexity O(logV))
Update path to w to be v, i.e. DT(w,1) = v
Example
In Figure 1A, A is the initial node and F is the goal destination node. The initial node starts with a tentative distance value of 0 while all other nodes start with infinity. To start we look at all neighboring nodes from A which are B,C and E. We then calculate the tentative distance for each of these nodes, B is the min (∞, 0+4) = 4; C is the min(∞,0+3)=3, E is the min ( ∞, 0+7) = 7. Out of all the neighboring nodes, C has the shortest distance, so C becomes the current node and we add C to the visited list. Then the process repeats. We look at the neighboring nodes of C which are B, D and E. B is the min ( 4, 6+3) = 4; D is min (∞, 3+11)=14; E is min(7, 3+8) = 7. In this round B has the smallest tentative distance so we visit B who only has neighbor of D since C has been visited. D is the min ( 14, 4+5 ) = 9 but E has not been visited and has a weight of 7 which is less than 9, so we visit node E. E as the current node, D and G have not been visited, so D is the min ( 9, 2+7)=9; G is the min(∞,7+5)=12. Therefore, we visit D which was calculated from A to B to D . Then, lastly F is the min ( ∞, 9+2)=11 so we visit F because G has a value of 12. Therefore, the path is from A to B to D to F.
Dijkstra’s algorithm fails to work if it encounters negative cycles or negative edges.However, this problem can be solved using Bellman-Ford algorithm.
Example when Dijkstra’s algorithm (with min-heap priority queue) fails:
Firstly in Figure 1B, the source vertex A is popped out of the queue and edges (A, C) and (A, B) are relaxed.
Secondly in Figure 2B, we have B on the top of our min-heap. Our algorithm now pops B and relaxes the only edge out of B i.e. (B, D) and thus we get distance of D = 3 + 1 = 4.
Now, we have vertex D, shown in Figure 3B on the top of the min-heap and we remove vertex D. Also, we don’t have any edges going out of D to relax. The only vertex left in the queue is C. We now remove C and relax the edge (C, B). Since, we have 5 - 4 = 1 < 3, distance to B must be updated to 1.
The algorithm will now terminate because our queue has become empty. However, our path from A -> C -> B -> D has a total length of 5 + (-4) + 1 = 2 < 4 as shown in Figure 4B. Therefore, clearly Dijkstra’s algorithm fails to correctly evaluate shortest path from A to D.
Variations
In some sense Dijkstra may be viewed as one of the most fundamental algorithms for solving the shortest path problem. There are numerous variants and extensions of Dijkstra algorithm; moreover, Dijkstra can be also often modified to solve various problem-specific tasks, therefore, we will concentrate only on one of the most famous variants of Dijkstra. In general, there are 3 main aspects of Dijkstra algorithms that can be modified or extended: Distance (distance meaning and evaluation between vertices and from a given vertex to final destination), underlying Data Structure (binary heap priority queue, for example, may be slightly modified or substituted completely with another data structure like list), and finally Relaxation and Distance Initialization (method of evaluating the opportunity of possible path improvement and method of initializing all distances between vertices respectively).
As we mentioned, some different types of modification are dependent on the problem to be solved, so for simplicity we will use a problem of finding shortest path between cities (represented by vertices) as an example, since it is most common and intuitive to understand.
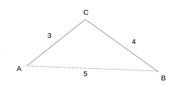
One of the most common modifications of Dijkstra is the Greedy Best First Search approach. Such an algorithm is driven by exactly same idea as Dijkstra (or in some sense Dijkstra, being part of BFS algorithms family, can be seen as a modification of Greedy Best First Search, but this is not the topic of our discussion), but instead of using the actual distances between vertices, it uses a so-called heuristic function that abstracts these distances. The choice of a heuristic function may vary and again is dependent on the type of a problem, but one possibility is to use shortest distances (think in terms of planar geometry, not in terms of actuals roads) from a city to a final destination. In Figure 5 the actual roads are bold lines, so using the described heuristic the distance from A (assuming B is the destination vertex) would be the length of straight (dashed) line between A and B:
Such algorithm offers an ease of computation and sometimes yields better (faster search) performance, however, as most of the algorithms that are based entirely on heuristics, does not guarantee to find the best (the shortest path) solution or even reach the final destination.
The next common extension of Dijkstra is A* algorithm, which is very similar to Greedy Best First Search, but uses both heuristic function and the actual distances between vertices. A* is considered to be one of the most popular and powerful short path algorithms and is often preferred to Dijkstra, as its use of heuristics can significantly increase the performance.
The next well-known algorithm that relies on the Dijkstra algorithm is Johnson's algorithm. Johnson's algorithm uses Bellman-Ford algorithm to deal with negative weights and transform the input graph into one that can be processed by Dijkstra algorithm. Johnson's implementation also uses Fibonacci-heap min priority queue instead of a Binary Heap, which yields not only exposure to a larger set of problems, but also a better performance.
As mentioned earlier the most common implementation of Dijkstra algorithm uses binary heap as its underlying data structure. There are, however, numerous modifications that could be made to the data structure in order to increase the performance or satisfy a particular goal. The most popular modifications include Dijkstra algorithm with Fibonacci heap, list, indexed priority queue, D-way heap and array. We compare run time complexity later in the discussion, but in general an array implementation is often used when dealing with dense graphs, while binary heap is significantly better performance-wise with sparse graphs. D-way head reduces computational cost compared to a binary heap, while Fibonacci heap, being extremely difficult in implementation, theoretically yields one of the best performances amongst all other Dijkstra modifications.
Time Complexity Analysis
The most commonly used Dijkstra’s algorithm uses binary heap. However, the running time complexity of variants/modification of Dijkstra’s algorithm depends on the way it is implemented. The Dijkstra’s algorithm can be implemented more efficiently if we store the graph in the form of adjacency list and using balancing binary search tree/ binary heap/ pairing heap/ fibonacci heap as our priority queue to implement extracting minimum efficiently.
Since, the algorithm fundamentally depends on time complexity of Extract-Min and Decrease-Key operation described in the pseudocode earlier, the time complexity of the Dijkstra’s algorithm can be generally be given by:
Θ (V) Textract-min + Θ (E) Tdecrease-key
Therefore, if we use a simple linked list or array to store the vertex set, and if our extract-minimum operation is a simple linear search through all the vertices, the running time is O (E + V ^2) = O (V^2).
The most commonly implemented Dijkstra’s algorithm uses a binary heap priority queue, the complexity of this algorithm is O (E logV + V logV) = O ((E + V)log(V)) = O (ElogV) because V is O (E).
Finally, if we use a more complicated priority queue called Fibonacci Heap, the asymptotic complexity of Dijkstra’s algorithm reduces to O (E + V log V).
There is a an specialized variant of Dijkstra’s algorithm which uses a special priority queue structure by Van Emde Boas in which edge weights are integers bounded by some constant C. This variant brings the complexity down to O (E log log |C|). Also, there is an another implementation of Dijkstra’s algorithm which uses a combination of radix heap and fibonacci heap. The running time of this implementation is O (E + V (log C)^0.5).
The running time complexity of Bellman-Ford algorithm which works with negative edges (and Dijkstra’s algorithm fails) is O (E V).
We have briefly covered one of the most famous and influential variants and extensions of Dijkstra algorithm, but it can be clearly seen that many more exist and could be created in order to satisfy particular needs of a developer.
References:
http://www.cse.unsw.edu.au/~cs2011/05s2/assignment4-solutions.pdf
http://faculty.simpson.edu/lydia.sinapova/www/cmsc250/LN250_Weiss/L27-GraphSummary.htm
https://en.wikipedia.org/wiki/Shortest_path_problem
http://www.csl.mtu.edu/cs2321/www/newLectures/30_More_Dijkstra.htm
https://www.cs.princeton.edu/~rs/AlgsDS07/15ShortestPaths.pdf
https://www.youtube.com/watch?v=gdmfOwyQlcI
https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm
https://en.wikipedia.org/wiki/Edsger_W._Dijkstra#Algorithmic_work
http://www.codeproject.com/Articles/19919/Shortest-Path-Problem-Dijkstra-s-Algorithm