| (33 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
== Classifying Platonic solids via subgroups of SO(3) == | == Classifying Platonic solids via subgroups of SO(3) == | ||
| − | by Lance Von Ah | + | by Lance Von Ah (lvonah@purdue.edu) |
[[Image:ALHdhMs.gif]] | [[Image:ALHdhMs.gif]] | ||
| + | |||
| + | Figure 1: The Platonic Solids | ||
| Line 75: | Line 77: | ||
| 3 | | 3 | ||
|} | |} | ||
| + | |||
| + | |||
| + | The Platonic Solids are proven to be convex polyhedra from Euler's characteristic: X = V - E + F. Any convex polyhedra's surface has a characteristic X = 2, which all five of the Platonic Solids do. | ||
'''What is the group SO(3)?''' | '''What is the group SO(3)?''' | ||
| − | The special orthogonal group SO(3) is the group of all rotations of R3 about a fixed origin. These rotations about the origin will not only preserve the origin, but also distance. It uses composition (the application of one function to another to produce a third function) as its operation. Every rotation within the SO(3) group, also has an inverse rotation, which would return an object to its original position. Any isometry which preserves the origin is a linear transformation, so if we were to classify the Platonic Solids based on the subgroups of SO(3), we are only worried about groups of rotations with a result about linear groups | + | The special orthogonal group SO(3) is the group of all rotations of R3 about a fixed origin. These rotations about the origin will not only preserve the origin, but also distance. It uses composition (the application of one function to another to produce a third function) as its operation. Every rotation within the SO(3) group, also has an inverse rotation, which would return an object to its original position. Any isometry which preserves the origin is a linear transformation, so if we were to classify the Platonic Solids based on the subgroups of SO(3), we are only worried about groups of rotations with a result about linear groups. |
| + | |||
| + | '''What are the finite subgroups of SO(3)?''' | ||
| + | |||
| + | ''Any finite subgroup of SO(3) is either a cycle group Cn a dihedral group Dn or one of the groups of a Platonic solid.'' Why is this so? Well, let G be a finite subgroup of SO(3) with order n. Then G acts on the unit sphere S and each rotation has two fixed points: its poles. We will look at the set of all poles on S (a finite set). | ||
| + | |||
| + | ''Every element of G maps a pole to a pole.'' This can proven by using p as a fixed point of an element g ∈ G and h as any element of G, then h*p is a fixed point of h*g*h^-1 ∈ G and hence is a pole. We then divide the set of poles into orbits: subsets of the form G*p for some pole p. | ||
| + | |||
| + | ''If p is a pole of an element of G of maximal order m then the orbit of p contains n/m elements.'' Why is this so? The subgroup H of G which leaves p fixed has m elements. So G is a union of cosets g1*H, g2*H, ... , gr*H with r = n/m. | ||
| + | All the elements in a coset gi*H will move p to the same point gip for i = 1, 2, ... , r. | ||
| + | Note that if i ≠ j then gip ≠ gjp since if gi * p = gj * p then gi^-1 * gj * p = p and so gi^-1 * gj ∈ H and so gi and gj would represent the same coset. | ||
| + | Hence the orbit of p is the set {g1*p, g2*p, ... , gr*p} as we said before. | ||
| + | |||
| + | The n - 1 non-zero rotations in G consist of m - 1 rotations for each pair of poles. | ||
| + | That is 1/2 (m - 1) n/m for each orbit. | ||
| + | Hence n - 1 = 1 /2 n(∑ (m-1)/m) where the summation is over the orbits ⇒ 2 - 2 /n = ∑ (1 - 1 /m ). | ||
| + | Since m ≥ 2 we have 1 - 1/m > 1/2 and so we can only have '''2 or 3 orbits if G is non-trivial'''. | ||
| + | |||
| + | '''The case of two orbits''' | ||
| + | |||
| + | Suppose these have n/m1 and n/m2 elements. | ||
| + | Then 2/n = 1/m1 + 1/m2 ⇒ 2 = n/m1 + n/m2 ⇒ (since m1 and m2 divide n) n/m1 = n/m2 = 1 and we have two orbits with one pole in each. This is the case when G is a cyclic group Cn created by rotation by 2π/n. Since this is the cyclic group, it is not isomorphic with the Platonic Solids. | ||
| + | |||
| + | '''The case of three orbits''' | ||
| + | |||
| + | 1 + 2/n = 1/m1 + 1/m2 + 1/m3. | ||
| + | We must have (say) m3 = 2 ⇒ 1/m1 + 1/m2 = 1/2 + 2/n ⇒ (m1 - 2)*(m2 - 2) = 4(1 - m1m2/n) < 4 | ||
| + | |||
| + | There are only a few possibilities: | ||
| + | m1 = 2, m2 = m, n = 2m (This is the dihedral case, which is not isomorphic with the Platonic Solids) | ||
| + | |||
| + | m1 = 3, m2 = 3, n = 12 (The tetrahedral case A(4)) | ||
| + | |||
| + | m1 = 3, m2 = 4, n = 24 (The octahedral case S(4)) | ||
| + | |||
| + | m1 = 3, m2 = 5, n = 60 (The dodecahedral case A(5)) | ||
| + | |||
| + | So for classifying the Platonic solids we care about these 3 symmetry groups: | ||
| + | |||
| + | '''Case 1: m1 = 3, m2 = 3, n = 12 (The tetrahedral case A(4))''' | ||
| + | |||
| + | '''Case 2: m1 = 3, m2 = 4, n = 24 (The octahedral case S(4))''' | ||
| + | |||
| + | '''Case 3: m1 = 3, m2 = 5, n = 60 (The dodecahedral case A(5))''' | ||
| + | |||
| + | '''Why only 3 cases when there are 5 Platonic solids?''' | ||
| + | |||
| + | There are only three symmetry groups, as opposed to five, because each Platonic solid is in a symmetry group with its dual solid. A dual solid is a solid that can be constructed from opposing dual solid by connecting vertices placed at the centers of each face. To sum it up, dual solids are a pair of solids where the faces and the vertices are switched. The tetrahedron is a dual with itself. The hexahedron/cube is a dual with the octahedron. The dodecahedron is a dual with the icosahedron. | ||
| + | |||
| + | '''Classification of the Platonic Solids:''' | ||
| + | |||
| + | {| class="wikitable" border="1" | ||
| + | |- | ||
| + | ! Platonic Solid | ||
| + | ! Symmetry Group | ||
| + | ! Order | ||
| + | ! Dual | ||
| + | |- | ||
| + | | Tetrahedron | ||
| + | | A(4) | ||
| + | | 12 | ||
| + | | Tetrahedron | ||
| + | |- | ||
| + | | Hexahedron(Cube) | ||
| + | | S(4) | ||
| + | | 24 | ||
| + | | Octahedron | ||
| + | |- | ||
| + | | Octahedron | ||
| + | | S(4) | ||
| + | | 24 | ||
| + | | Hexahedron | ||
| + | |- | ||
| + | | Dodecahedron | ||
| + | | A(5) | ||
| + | | 60 | ||
| + | | Icosahedron | ||
| + | |- | ||
| + | | Icosahedron | ||
| + | | A(5) | ||
| + | | 60 | ||
| + | | Dodecahedron | ||
| + | |} | ||
| + | |||
| + | [[Image:dualsolid.jpg|400px]] | ||
| + | |||
| + | Figure 2: The duals of the Platonic Solids | ||
| + | |||
| + | |||
| + | '''Where would we see Platonic Solids?''' | ||
| + | |||
| + | Most commonly in daily life you can see the Platonic Solids in the form of dice. They make excellent dice because the symmetry of the Platonic Solid allows to be a fair dice (a dice in which all possibilities are equally likely). With the five solids you can make 4, 6, 8, 12 and 20 sided dice. The tetrahedron, hexahedron, and the octahedron all occur naturally in crystal structures. They are by no means the extent of all crystal structures but there symmetry is found in nature. Also, many viruses take on the shape of an icosahedron. Because viral structures are built from repeating protein subunits, the icosahedron is the easiest shape to be created using the shape of those subunits. | ||
| + | |||
| + | [[Image:dice.jpg]] | ||
| + | |||
| + | Figure 3: Dice made from the five Platonic Solids | ||
| + | |||
| + | [[Image:Virus.jpg]] | ||
| + | |||
| + | Figure 4: A virus (Circogonia icosahedra) shaped liked an icosahedron | ||
| + | |||
| + | |||
| + | |||
| + | '''References''' | ||
| + | |||
| + | Mark, Hannah. August 23, 2011. "CLASSIFYING FINITE SUBGROUPS OF SO3": http://www.math.uchicago.edu/~may/VIGRE/VIGRE2011/REUPapers/MarkH.pdf | ||
| + | |||
| + | "Symmetry groups of Platonic Solids" February 2010: http://www-history.mcs.st-and.ac.uk/~john/MT4521/Lectures/L10.html | ||
| + | |||
| + | I. BUSJATSKAYA AND M. MONASTYRSKY. "IMMORTALITY OF PLATONIC SOLIDS": http://www.newton.ac.uk/preprints/NI13017.pdf | ||
| + | |||
| + | http://groupprops.subwiki.org/wiki/Classification_of_finite_subgroups_of_SO(3,R)#Basic_statement | ||
| + | ''The Geometry Junkyard'', "Twenty Proofs of Euler's Formula: V-E+F=2": http://www.ics.uci.edu/~eppstein/junkyard/euler/ | ||
| + | http://en.wikipedia.org/wiki/Platonic_solid#cite_note-The_Stanford_Encyclopedia_of_Philosophy-1 | ||
| + | http://en.wikipedia.org/wiki/Rotation_group_SO(3)#cite_note-1 | ||
| + | "Platonic Solids" : http://whistleralley.com/polyhedra/platonic.htm | ||
| + | http://mathworld.wolfram.com/PlatonicSolid.html | ||
| + | "Why Only Five?" Feature Column from the AMS. : http://www.ams.org/samplings/feature-column/fcarc-five-polyhedra | ||
Latest revision as of 10:36, 2 December 2013
Classifying Platonic solids via subgroups of SO(3)
by Lance Von Ah (lvonah@purdue.edu)
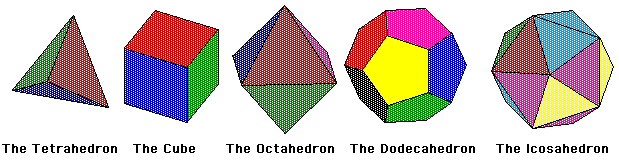
Figure 1: The Platonic Solids
What are Platonic Solids?
The Platonic Solids are the only regular convex polyhedra. This means they are an object bounded by planes in R3, in which all its faces are congruent regular polygons and the same number of faces meet at each vertex. There are only five of these objects; the tetrahedron, the hexahedron (or cube), the octahedron, the dodecahedron, and the icosahedron. These objects were very intriguing to the ancient Greeks who found their symmetry fascinating. They became known as the Platonic solids from the Greek philosopher Plato who theorized the four classical elements (Air, Fire, Water, and Earth) were made from these solids.
Why only 5 Platonic solids?
Euclid argues in Book XIII of Elements that there can only be five platonic solids and no others possible. He does so by giving a geometric argument which is outlined below:
1. Each vertex of the solid must be made up by the edge of three or more faces.
2. At each vertex of the solid, the sum of the angles formed by the faces at a vertex need to be less than 360 degrees.
3. Since there needs to be three or more faces at each vertex and each face’s angle is the same, then the angles of all the faces of the solid must be less than 120 degrees.
4. Possible faces of the solid:
•Regular Triangle: each angle of a regular triangle is 60 degrees, so a Platonic Solid may have a vertex where 3 triangles (tetrahedron), 4 triangles (octahedron), or 5 triangles (icosahedron) meet. 6 triangles meeting at a vertex result in an angle of 360 degrees which could not create a 3D object.
•Regular Square: each angle of a regular square is 90 degrees, so a Platonic Solid may have a vertex where 3 squares meet (hexahedron). Like 6 triangles, 4 squares meeting a vertex result in an angle of 360 degrees.
•Regular Pentagon: each angle of a regular pentagon is 108 degrees, so a Platonic Solid may have a vertex where 3 pentagons meets (dodecahedron).
•Regular Polygons with more than 5 sides: each angle of a regular polygon with more than 5 sides has an angle greater than or equal to 120 degrees. Thus, no Platonic Solid could be created from them.
Numberphile does a great visual demonstration of this proof: [1]
| Platonic Solid | Number of faces (F) | Number of edges (E) | Number of vertices (V) | Edges per face |
|---|---|---|---|---|
| Tetrahedron | 4 | 6 | 4 | 3 |
| Hexahedron(Cube) | 6 | 12 | 8 | 4 |
| Octahedron | 8 | 12 | 6 | 3 |
| Dodecahedron | 12 | 30 | 20 | 5 |
| Icosahedron | 20 | 30 | 12 | 3 |
The Platonic Solids are proven to be convex polyhedra from Euler's characteristic: X = V - E + F. Any convex polyhedra's surface has a characteristic X = 2, which all five of the Platonic Solids do.
What is the group SO(3)?
The special orthogonal group SO(3) is the group of all rotations of R3 about a fixed origin. These rotations about the origin will not only preserve the origin, but also distance. It uses composition (the application of one function to another to produce a third function) as its operation. Every rotation within the SO(3) group, also has an inverse rotation, which would return an object to its original position. Any isometry which preserves the origin is a linear transformation, so if we were to classify the Platonic Solids based on the subgroups of SO(3), we are only worried about groups of rotations with a result about linear groups.
What are the finite subgroups of SO(3)?
Any finite subgroup of SO(3) is either a cycle group Cn a dihedral group Dn or one of the groups of a Platonic solid. Why is this so? Well, let G be a finite subgroup of SO(3) with order n. Then G acts on the unit sphere S and each rotation has two fixed points: its poles. We will look at the set of all poles on S (a finite set).
Every element of G maps a pole to a pole. This can proven by using p as a fixed point of an element g ∈ G and h as any element of G, then h*p is a fixed point of h*g*h^-1 ∈ G and hence is a pole. We then divide the set of poles into orbits: subsets of the form G*p for some pole p.
If p is a pole of an element of G of maximal order m then the orbit of p contains n/m elements. Why is this so? The subgroup H of G which leaves p fixed has m elements. So G is a union of cosets g1*H, g2*H, ... , gr*H with r = n/m. All the elements in a coset gi*H will move p to the same point gip for i = 1, 2, ... , r. Note that if i ≠ j then gip ≠ gjp since if gi * p = gj * p then gi^-1 * gj * p = p and so gi^-1 * gj ∈ H and so gi and gj would represent the same coset. Hence the orbit of p is the set {g1*p, g2*p, ... , gr*p} as we said before.
The n - 1 non-zero rotations in G consist of m - 1 rotations for each pair of poles. That is 1/2 (m - 1) n/m for each orbit. Hence n - 1 = 1 /2 n(∑ (m-1)/m) where the summation is over the orbits ⇒ 2 - 2 /n = ∑ (1 - 1 /m ). Since m ≥ 2 we have 1 - 1/m > 1/2 and so we can only have 2 or 3 orbits if G is non-trivial.
The case of two orbits
Suppose these have n/m1 and n/m2 elements. Then 2/n = 1/m1 + 1/m2 ⇒ 2 = n/m1 + n/m2 ⇒ (since m1 and m2 divide n) n/m1 = n/m2 = 1 and we have two orbits with one pole in each. This is the case when G is a cyclic group Cn created by rotation by 2π/n. Since this is the cyclic group, it is not isomorphic with the Platonic Solids.
The case of three orbits
1 + 2/n = 1/m1 + 1/m2 + 1/m3. We must have (say) m3 = 2 ⇒ 1/m1 + 1/m2 = 1/2 + 2/n ⇒ (m1 - 2)*(m2 - 2) = 4(1 - m1m2/n) < 4
There are only a few possibilities: m1 = 2, m2 = m, n = 2m (This is the dihedral case, which is not isomorphic with the Platonic Solids)
m1 = 3, m2 = 3, n = 12 (The tetrahedral case A(4))
m1 = 3, m2 = 4, n = 24 (The octahedral case S(4))
m1 = 3, m2 = 5, n = 60 (The dodecahedral case A(5))
So for classifying the Platonic solids we care about these 3 symmetry groups:
Case 1: m1 = 3, m2 = 3, n = 12 (The tetrahedral case A(4))
Case 2: m1 = 3, m2 = 4, n = 24 (The octahedral case S(4))
Case 3: m1 = 3, m2 = 5, n = 60 (The dodecahedral case A(5))
Why only 3 cases when there are 5 Platonic solids?
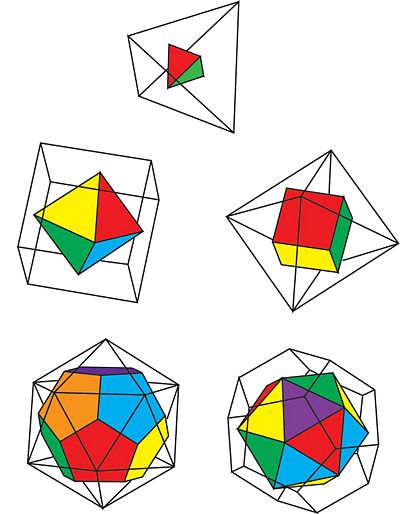
There are only three symmetry groups, as opposed to five, because each Platonic solid is in a symmetry group with its dual solid. A dual solid is a solid that can be constructed from opposing dual solid by connecting vertices placed at the centers of each face. To sum it up, dual solids are a pair of solids where the faces and the vertices are switched. The tetrahedron is a dual with itself. The hexahedron/cube is a dual with the octahedron. The dodecahedron is a dual with the icosahedron.
Classification of the Platonic Solids:
| Platonic Solid | Symmetry Group | Order | Dual |
|---|---|---|---|
| Tetrahedron | A(4) | 12 | Tetrahedron |
| Hexahedron(Cube) | S(4) | 24 | Octahedron |
| Octahedron | S(4) | 24 | Hexahedron |
| Dodecahedron | A(5) | 60 | Icosahedron |
| Icosahedron | A(5) | 60 | Dodecahedron |
Figure 2: The duals of the Platonic Solids
Where would we see Platonic Solids?
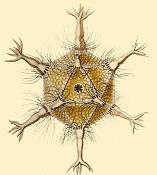
Most commonly in daily life you can see the Platonic Solids in the form of dice. They make excellent dice because the symmetry of the Platonic Solid allows to be a fair dice (a dice in which all possibilities are equally likely). With the five solids you can make 4, 6, 8, 12 and 20 sided dice. The tetrahedron, hexahedron, and the octahedron all occur naturally in crystal structures. They are by no means the extent of all crystal structures but there symmetry is found in nature. Also, many viruses take on the shape of an icosahedron. Because viral structures are built from repeating protein subunits, the icosahedron is the easiest shape to be created using the shape of those subunits.
Figure 3: Dice made from the five Platonic Solids
Figure 4: A virus (Circogonia icosahedra) shaped liked an icosahedron
References
Mark, Hannah. August 23, 2011. "CLASSIFYING FINITE SUBGROUPS OF SO3": http://www.math.uchicago.edu/~may/VIGRE/VIGRE2011/REUPapers/MarkH.pdf
"Symmetry groups of Platonic Solids" February 2010: http://www-history.mcs.st-and.ac.uk/~john/MT4521/Lectures/L10.html
I. BUSJATSKAYA AND M. MONASTYRSKY. "IMMORTALITY OF PLATONIC SOLIDS": http://www.newton.ac.uk/preprints/NI13017.pdf
http://groupprops.subwiki.org/wiki/Classification_of_finite_subgroups_of_SO(3,R)#Basic_statement
The Geometry Junkyard, "Twenty Proofs of Euler's Formula: V-E+F=2": http://www.ics.uci.edu/~eppstein/junkyard/euler/
http://en.wikipedia.org/wiki/Platonic_solid#cite_note-The_Stanford_Encyclopedia_of_Philosophy-1
http://en.wikipedia.org/wiki/Rotation_group_SO(3)#cite_note-1
"Platonic Solids" : http://whistleralley.com/polyhedra/platonic.htm
http://mathworld.wolfram.com/PlatonicSolid.html
"Why Only Five?" Feature Column from the AMS. : http://www.ams.org/samplings/feature-column/fcarc-five-polyhedra
--Lvonah 12:41, 1 December 2013 (UTC)