(→Fisher's Formula in brief: added projection) |
|||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
==Introduction== | ==Introduction== | ||
| − | Fisher's linear discriminant is a classification method that projects high-dimensional data onto a line and performs classification in this one-dimensional space. The projection maximizes the distance between the means of the two classes while minimizing the variance within each class. See [Lecture | + | Fisher's linear discriminant is a classification method that projects high-dimensional data onto a line and performs classification in this one-dimensional space. The projection maximizes the distance between the means of the two classes while minimizing the variance within each class. See [[Lecture 10_OldKiwi]] for detailed explanation. |
| + | |||
| + | == Fisher's Formula in brief == | ||
| + | Main article: [[Derivation of Fisher's Linear Discriminant_OldKiwi]] | ||
| + | |||
| + | Fisher's Linear Discriminant maximizes <math>J(\vec{w})=\frac {{\vec{w}}^{T}{S}_{B}\vec{w}} {{\vec{w}}^{T}{S}_{W}\vec{w}}</math>, explicit function of <math>\vec{w}</math> | ||
| + | |||
| + | |||
| + | where, <math>S_B = (m_1-m_2)(m_1^T-m_2^T)</math> is 'between class scatter matrix'. | ||
| + | |||
| + | and, <math>S_w = \displaystyle \sum_{\vec y \; in \; class} (y_i-m_i)(y_i^T-m_i^T) </math> is 'within class scattter matrix'. | ||
| + | |||
| + | |||
| + | Fisher's Discriminant projects the data as in the following equation | ||
| + | |||
| + | <math>\omega = S_w^{-1} (m_1-m_2)</math> | ||
| + | |||
| + | <math>\hat{x} = \omega^T x</math> | ||
| + | |||
| + | Then we can classify the data using | ||
| + | |||
| + | <math>\hat{x}>\hat{x}_0</math> | ||
| + | |||
| + | where | ||
| + | |||
| + | <math>\hat{x_0} = \omega^T(m_1+m_2)/2</math> | ||
==Finding the separating hyperplane and finding the projection direction are dual problems== | ==Finding the separating hyperplane and finding the projection direction are dual problems== | ||
| − | Fisher's Linear Discriminant relies on dimension reduction. If we want to project D-dimensional data down to one dimension we can use <math>y=\omega^T \vec{x}</math> . After that, by determining a threshold <math>\omega_0</math>, we can select class 1 if <math>y>\omega_0</math> and class 2 if <math>y<\omega_0 | + | Fisher's Linear Discriminant relies on dimension reduction. If we want to project D-dimensional data down to one dimension we can use <math>y=\omega^T \vec{x}</math> . After that, by determining a threshold <math>\omega_0</math>, we can select class 1 if <math>y>\omega_0</math> and class 2 if <math>y<\omega_0</math>. |
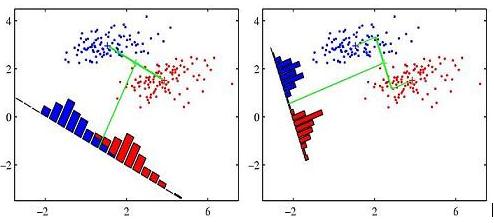
However, dimension reduction can cause considerable amount of information loss leading not being able to separate the data in reduced dimension, while the data is separable in D dimension. Fisher's Linear Discriminant method uses that idea by adjusting the weight vector <math>\omega</math> for projection to minimize the amount of overlapping data in reduced dimension. Here are some figures from C. M. Bishop's book to understand the idea completely. | However, dimension reduction can cause considerable amount of information loss leading not being able to separate the data in reduced dimension, while the data is separable in D dimension. Fisher's Linear Discriminant method uses that idea by adjusting the weight vector <math>\omega</math> for projection to minimize the amount of overlapping data in reduced dimension. Here are some figures from C. M. Bishop's book to understand the idea completely. | ||
| Line 25: | Line 50: | ||
==References== | ==References== | ||
| − | " | + | "[http://ieeexplore.ieee.org/Xplore/login.jsp?url=/iel5/34/21179/00982904.pdf Two variations on Fisher's linear discriminant for pattern recognition]" is a nice journal article. The paper provides two fast and simple techniques for improving on the classification performance provided by Fisher's linear discriminant for two classes. |
| − | See the following link for the detailed information: | + | |
| − | + | See the following link for the detailed information: [http://ieeexplore.ieee.org/Xplore/login.jsp?url=/iel5/34/21179/00982904.pdf Two variations on Fisher's linear discriminant for pattern recognition]. | |
Latest revision as of 18:05, 28 March 2008
Contents
Introduction
Fisher's linear discriminant is a classification method that projects high-dimensional data onto a line and performs classification in this one-dimensional space. The projection maximizes the distance between the means of the two classes while minimizing the variance within each class. See Lecture 10_OldKiwi for detailed explanation.
Fisher's Formula in brief
Main article: Derivation of Fisher's Linear Discriminant_OldKiwi
Fisher's Linear Discriminant maximizes $ J(\vec{w})=\frac {{\vec{w}}^{T}{S}_{B}\vec{w}} {{\vec{w}}^{T}{S}_{W}\vec{w}} $, explicit function of $ \vec{w} $
where, $ S_B = (m_1-m_2)(m_1^T-m_2^T) $ is 'between class scatter matrix'.
and, $ S_w = \displaystyle \sum_{\vec y \; in \; class} (y_i-m_i)(y_i^T-m_i^T) $ is 'within class scattter matrix'.
Fisher's Discriminant projects the data as in the following equation
$ \omega = S_w^{-1} (m_1-m_2) $
$ \hat{x} = \omega^T x $
Then we can classify the data using
$ \hat{x}>\hat{x}_0 $
where
$ \hat{x_0} = \omega^T(m_1+m_2)/2 $
Finding the separating hyperplane and finding the projection direction are dual problems
Fisher's Linear Discriminant relies on dimension reduction. If we want to project D-dimensional data down to one dimension we can use $ y=\omega^T \vec{x} $ . After that, by determining a threshold $ \omega_0 $, we can select class 1 if $ y>\omega_0 $ and class 2 if $ y<\omega_0 $.
However, dimension reduction can cause considerable amount of information loss leading not being able to separate the data in reduced dimension, while the data is separable in D dimension. Fisher's Linear Discriminant method uses that idea by adjusting the weight vector $ \omega $ for projection to minimize the amount of overlapping data in reduced dimension. Here are some figures from C. M. Bishop's book to understand the idea completely.
Context: Classical Discriminant Analysis_OldKiwi Problem
Given data $ y_1,\cdots, y_d \in \mathbb{R}^n $, from 2 classes. When n is big, it may be difficult to separate classes, because of computational issues.
In this case we try to find a projection $ \pi: R^n \rightarrow R^k, k <n $ s.t . $ \pi(y_1), \cdots, \pi(y_d) $ can be separated.
Derivation of Fisher's Linear Discriminant
Main article: Derivation of Fisher's Linear Discriminant_OldKiwi
References
"Two variations on Fisher's linear discriminant for pattern recognition" is a nice journal article. The paper provides two fast and simple techniques for improving on the classification performance provided by Fisher's linear discriminant for two classes.
See the following link for the detailed information: Two variations on Fisher's linear discriminant for pattern recognition.