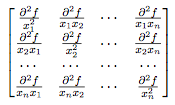(New page: The Hessian of a function (denoted <math>F(x_1, x_2, \cdots , x_n)</math>) is the multivariate equivalent to the second derivative of a single variable function. Similar to the [[gradient]...) |
|||
| Line 2: | Line 2: | ||
[[Image:Hessian_OldKiwi.png]] | [[Image:Hessian_OldKiwi.png]] | ||
| + | |||
| + | [[Category:Linear Algebra]] | ||
Latest revision as of 10:40, 24 March 2008
The Hessian of a function (denoted $ F(x_1, x_2, \cdots , x_n) $) is the multivariate equivalent to the second derivative of a single variable function. Similar to the gradient_OldKiwi of a multivariate function, the Hessian is a square matrix where each entry is the composite of two partial differentiations. For a function $ f(x_1, x_2, \cdots , x_n) $, the Hessian is defined as: