| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | ==Part 1== | ||
| + | |||
A CT signal posted on Homework 1 was: | A CT signal posted on Homework 1 was: | ||
x(t) = sin(t) | x(t) = sin(t) | ||
| Line 21: | Line 23: | ||
Note: This isn't an exact representation, but I did the best I could estimating the points using paint. In any case, it it possible to see that the thick lines are not periodic. | Note: This isn't an exact representation, but I did the best I could estimating the points using paint. In any case, it it possible to see that the thick lines are not periodic. | ||
| + | |||
| + | |||
| + | ==Part 2== | ||
| + | |||
| + | ==Creation of a Periodic Signal from a Non Periodic signal== | ||
| + | A non-periodic function posted on hw 1 was: | ||
| + | |||
| + | x(t) = 2t+1 | ||
| + | |||
| + | To change this to be periodic we take the sum x(t+kT). Set T = 5 therefore our new signal is | ||
| + | x(t+5k) = 2(t+5k)+1 for all integer values of k. | ||
| + | |||
| + | Then we have a periodic signal which looks like: | ||
| + | |||
| + | [[Image:Repeated non periodic signal_ECE301Fall2008mboutin.JPG]] | ||
| + | |||
Back to Homework 2: | Back to Homework 2: | ||
[[Homework 2_ECE301Fall2008mboutin]] | [[Homework 2_ECE301Fall2008mboutin]] | ||
Latest revision as of 09:46, 11 September 2008
Contents
Part 1
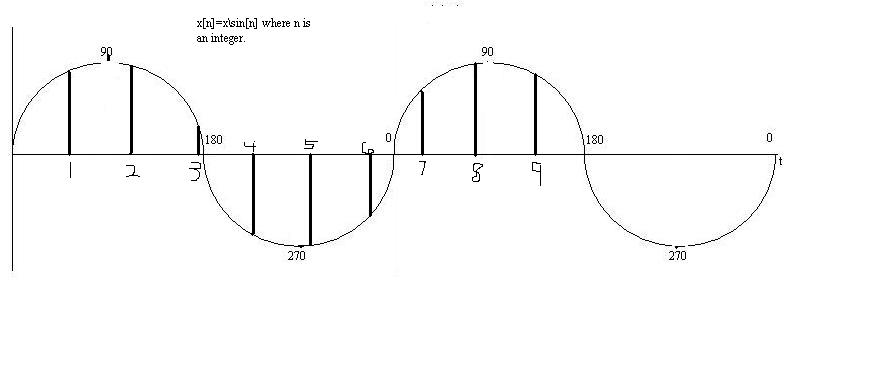
A CT signal posted on Homework 1 was: x(t) = sin(t)
Periodic Signal
The New DT Signal: x[n] = sin[n] So taking that signal and making it a periodic DT signal by sampling at frequencies of n where n can only be multiples of pi.
Non Periodic Signal
The new DT Signal: x[n] = sin[n] Making this signal non periodic is by simply taking n to integer numbers, n=1, n=2, n=3, etc.
Note: This isn't an exact representation, but I did the best I could estimating the points using paint. In any case, it it possible to see that the thick lines are not periodic.
Part 2
Creation of a Periodic Signal from a Non Periodic signal
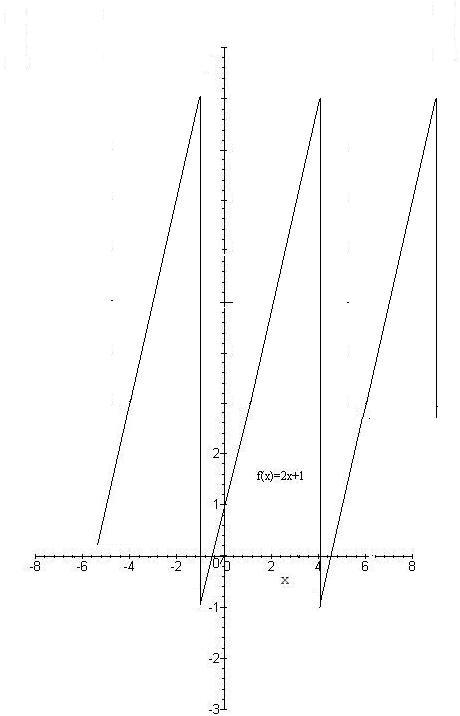
A non-periodic function posted on hw 1 was:
x(t) = 2t+1
To change this to be periodic we take the sum x(t+kT). Set T = 5 therefore our new signal is x(t+5k) = 2(t+5k)+1 for all integer values of k.
Then we have a periodic signal which looks like:
Back to Homework 2:
Homework 2_ECE301Fall2008mboutin