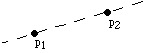| (7 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
Pinar Temiz (ptemiz@purdue.edu) | Pinar Temiz (ptemiz@purdue.edu) | ||
| − | = '''Origami | + | = '''Origami and Mathematics''' = |
| − | [[Image:P Swan Montroll Bringing.JPG]] | + | [[Image:P Swan Montroll Bringing.JPG]]<br> |
| − | + | Picture from Aharoni, 2013.<br> | |
| − | + | == Introduction/History of Origami == | |
| − | + | Origami, despite what many math believe, is orignally thought to have roots in China (PBS, 2009). This art form was brought to Japan from China. Coming from the Japanese words ''oru''(to fold) and ''kami''(paper)origami was only at first only available for the weathly since paper was so expensive. Since the expense was so great, oragami was mainly used for ceremonies and religious events. However, as time passed and paper was produced on a larger scale, origami became available for both the rich and poor. For the same reason, people starting creating origami for art instead of for ceremonial/religous purposes. For a long time this art form was simply passed down from one generation to the next without writing. In fact, the first written instructions were by Akisato Rito called "Thousand Crane Folding". Older forms of origami were simply paper folded to make a design such as a crane. However, modern origami is created by artists. Modern designs can even look like puzzles created by mathematicians. Akira Yoshizawa is considered one of the fathers of modern origami because he created a system of folding patterns, symbols, arrows, and diagrams to streamline this art. His methods are still being used today. Now, more and more people are creating this art using mathematical principles and ideas. The study of origami mathematics began in the 1980's (DeMaine, 2010). This field studies the properties of origami including what happens once you unfold a piece of origami. Many study the patterns and different properties the piece of unfolded paper has. A few of the "mathematical origami pioneers" include Jun Maekawa, Peter Engel, Robert Lang, and Erik Demaine. All of the mathematicians use particular constructs in order to create the amazing origami structures seen today. | |
| − | |||
| − | + | == Origami Mathematics == | |
| − | + | ===== <u>Related Mathematicians</u> ===== | |
| + | A related Mathemetician whose work is really interesting is Robert J. Lang. He has a very good way of explaining how origami works and how we use origami in everyday life even in ways we would not have even thought. For example, he came up with an idea to get a telescope with a lens with a diameter of 100 meters, which would be the size of a football field, into space to orbit around the Earth 22,000 miles away (Lang, 2013). Lang knew that the bigger the telescope was, the better and sharper the images would be and hence he tried to make it as big as it could be with still being able to take it up into space and the idea was the it would be a thin as a sheet of paper. All space vehicles, such as heavy lift rockets, usually had a capacity to carry objects of a 4 meter diameter and that is 10 meters long. This meant that the lens had to be folded, crumpled or stuffed into the tube of the rocket. However, if there was an undesired fold then this would ruin the optical performance of the lens, therefore it had to have to be collapsed into a smaller shape by a controlled set of creases whose locations and structure would not degrade the optical performance. Robert Lang is also the developer of a computer program called TreeMaker which takes a stick figure drawing and creates a crease pattern to make the desired figure. Below, under "Examples" are the finished product of a flag, frog, and spider all created from the program TreeMaker. This program actually uses a mathematical algorithm and properties of origami figures to determine which particular creases and folds are needed in order to produce the finished piecel however, determine exactly how to fold and in what order is left to the designer. This program is interesting because Lang has even stated that the software allows him to create patterns that he would not otherwise be able to create with a pencil and paper. A link to download TreeMaker is available at the bottom of the page. | ||
| + | |||
| + | |||
| + | |||
| + | Erik DeMaine has interests in folding, or seeing how a given object such as paper can be "reconfigured or folded according to a few constraints" (DeMaine, 2010). The ultimate goal with his research is to determine an algorith for characterizing different aspects of foldability for an object or showing that no such algorithm is possible. One result in folding is something called "universal results" where in a particular model of folding, everything is possible. If "universal results" are not possible, the next best option is an "efficient algorithm" that helps determine if an object is foldable. DeMaine does not only work with origami, he has also done research in the foldings of other objects such as proteins or polyhedrons. This work is useful in the field of origami mathematics because it can help create the properties of a given piece of origami. As the field continues to develop and grow, more information will be discovered about the particular properties that make up pieces of origami. | ||
| + | |||
| + | <br> | ||
| + | |||
| + | ===== <u>Real Life Examples Using Mathematics and Origami</u> ===== | ||
| + | |||
| + | In the 1980’s origami had been used in space for a solar panel designed by Koryo Miura to fly in a Japanese satellite. There were different structures and ideas adapted for the Eyeglass telescope using origami and applying it to the telescope. They needed a radically symmetric structure and collapsed on a finite number of creases that fit within a cylindrical form factor such as a rocket. The origami structure that was settled with was called the ‘Umbrella’ as it resembled a collapsible umbrella which folded from a large flat disk down to a much smaller bordered cylinder. | ||
| + | |||
| + | <br> | ||
== How it works == | == How it works == | ||
| − | ''Huzita's Origami Axioms'' | + | ''Huzita's Origami Axioms'' |
1) Given two points p1 and p2 we can fold a line connecting them. | 1) Given two points p1 and p2 we can fold a line connecting them. | ||
| − | [[Image: | + | [[Image:Origami1.jpg]] |
| − | 2) Given two points p1 and p2 we can fold p1 onto p2. | + | 2) Given two points p1 and p2 we can fold p1 onto p2. |
| − | [[Image: | + | [[Image:Origami2.jpg]] |
| − | 3) Given two lines l1 and l2 we can fold line l1 onto l2. | + | 3) Given two lines l1 and l2 we can fold line l1 onto l2. |
| − | [[Image: | + | [[Image:Origami3.jpg]] |
| − | 4) Given a point p1 and a line l1 we can make a fold perpendicular to l1 passing through the point p1. | + | 4) Given a point p1 and a line l1 we can make a fold perpendicular to l1 passing through the point p1. |
| − | [[Image: | + | [[Image:Origami4.jpg]] |
| − | 5) Given two points p1 and p2 and a line l1 we can make a fold that places p1 onto l1 and passes through the point p2. | + | 5) Given two points p1 and p2 and a line l1 we can make a fold that places p1 onto l1 and passes through the point p2. |
| − | [[Image: | + | [[Image:Origami5.jpg]] |
| − | 6) Given two points p1 and p2 and two lines l1 and l2 we can make a fold that places p1 onto line l1 and places p2 onto line l2.
| + | 6) Given two points p1 and p2 and two lines l1 and l2 we can make a fold that places p1 onto line l1 and places p2 onto line l2.
|
| − | [[Image: | + | [[Image:Origami6.jpg]] |
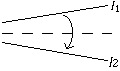
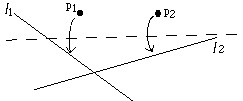
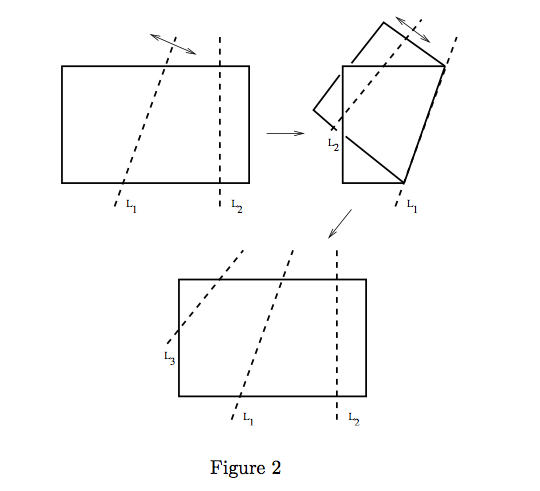
| + | <br> ''There are four natural methods to folding paper. The 1st, 2nd and 3rd methods are illustrated by figure 1 and the 4th method is illustrated by figure 2.'' | ||
| − | + | [[Image:Origamifigure1.png]] | |
| − | [[Image: | + | [[Image:Origamifigure2.png]] |
| − | + | Which are used for this definition below: | |
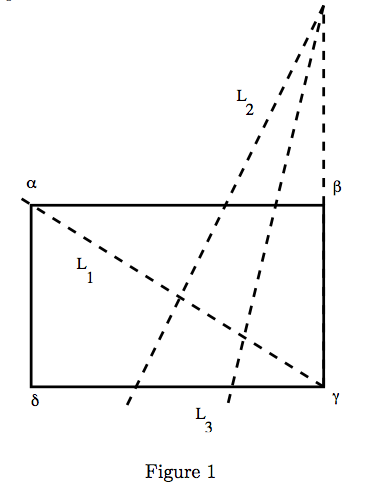
| − | + | ''(P,L) is an origami pair if P is a set of points in R2 and L is a collection of lines in R2 satisfying:'' | |
| − | '' | + | ''i) The point of intersection of any two non-parallel lines in L is a point in P.'' |
| − | '' | + | ''ii) Given any two distinct points in P, there is a line in L going through them.'' |
| − | '' | + | ''iii) Given any two distinct points in P, the perpendicular bisector of the line segment with given end points is a line in L.'' |
| − | '' | + | ''iv) If L1 and L2 are lines in L, then the line which is equidistant from L1 and L2 is in L.'' |
| − | '' | + | ''v) If L1 andL2 arelinesinL,thenthereexistsalineL3 inLsuchthatL3 isthe mirror reflection of L2 about L1.'' |
| − | + | <br> Origami and groups are introduced in the following two definitions: | |
| + | 1) A subset of R2,P, is closed under origami constructions if there exists a collection of lines, L, such that (P,L) is an origami pair. | ||
| − | + | 2) P0 = ∩{P | (0, 0), (0, 1) ∈ P and P is closed under origami constructions} is the set of origami constructible points. | |
| − | + | <br> | |
| − | + | == Relation to other fields of mathematics == | |
| + | Origami relates in many ways to different fields of mathematics. For example, many teachers in high schools use origami to teach many topics in their curriculum. Areas included are problem solving, geometry, ratios, angles. logic, proofs, congruence, properties of parallel lines, and the list goes on. (Serenevy, 2003). One example Robert Lang gave in his TED talk was the fact that any origami figure can be unfolded and colored using only 2 colors. This would be a good example to show in a discrete mathematics class in high school (Lang, 2013). There is also a fairly obvious connection to the field of geometry. Many geometric shapes and designs can be made with one sheet of square paper using different folds. Overall, even though the mathematics is starting to have a much deeper role in the creation of origami figures, there is a practical use for this math at a high school level relating to several different mathematical fields. | ||
| − | == | + | == Importance of Origami and Practicality of the Mathematics<br> == |
| − | Origami | + | Origami is used a lot in daily life and in a lot of varying things. When one generally thinks of origami, they usually think of the interesting and pretty shapes that it can create and and it has indeed been appreciated as a beautiful form of art for a very long time (there are examples of different and interesting pictures of origami below). Of course Origami has been used for many different other purposes one of which include teachers using it to teach their students about geometry and problem solving with other aspects of origami use being that of a method of therapy in all different medical fields. These include as a way to exercise hand muscles that are trying to rehabilitate and also for people who suffer from arthritis as it is seen as a good method to strengthen muscles. Also it is used in the psychology medical field and they have discovered that Origami can help with better memory, more creativity and imagination, a better attention span and even the development of their motor skills. It can also be used as a means to relieve stress also. Origami can also be used in different sciences and technology as well as art and sculptures and it is more part of our life than we may realise. Another very interesting real life use of origami is the use of transportable objects that reduce in their original size so that it is an easier way to carry them whilst you are on the move. For example in this article: http://www.cnn.com/2013/10/11/tech/innovation/folding-origami-oru-kayak/ it shows how these different methods of transport that can be folded to make it travel size. Below are the ones that we found the most interesting: |
| − | + | [[Image:Transport1.png]] | |
| − | + | [[Image:Transport2.png]] | |
| − | + | [[Image:Transport3.png]] | |
| − | + | ||
| − | + | ||
| − | [[Image: | + | [[Image:Transport4.png]] |
| + | |||
| + | [[Image:Transport5.png]] | ||
| + | |||
| + | <br> | ||
| + | |||
| + | ===== Practicality: ===== | ||
| + | |||
| + | In all honesty, the mathematics used to create the above examples has proven extremely practical in everyday life. Having these techniques allows us to do things with objects that we were not previously able to do. For example, using mathematics to create a folding telescope that is able to be sent to space. Using the axioms listed above, the telescope was allowed to be folded into a smaller version so it was easily able to be lifted into space. While there are many practical applications of the mathematics of origami, this math would probably be incredibly difficult for students in high school to understand unless the rules were simplified. A few of the rules, or interesting facts, such as an unfolded piece of origami can be 2-colored, would be helpful for students, but much of the math is difficult to understand and explain without advanced mathematics knowledge. | ||
| − | |||
| − | |||
| − | + | While these problems are mostly mathematical, they do have a way that can relate to real life. For example, Paul Earwicker posted this question: "We buy tea in square paper bags. These are sealed around all four edges. The question is what is the maximum volume that can be contained?". Principles of origami can be used to help solve this problem, showing that that these particular properties can be useful in everyday life. A link to the problem thread is included in the "Interesting Links" at the bottom of the page. | |
| − | |||
| − | |||
== Examples == | == Examples == | ||
| − | + | ===== The following are examples of origami figures as well as their crease patterns.<br>[[Image:Stars Stipes.jpg|left|2x1px]][[Image:Stars Stipes.jpg]] ===== | |
| − | + | ||
Flag from 1 sheet of paper | Flag from 1 sheet of paper | ||
| Line 136: | Line 152: | ||
http://www.ted.com/talks/robert_lang_folds_way_new_origami.html?quote=323 | http://www.ted.com/talks/robert_lang_folds_way_new_origami.html?quote=323 | ||
| + | |||
| − | + | - A link to download TreeMaker software by Robert Lang | |
| + | |||
| + | http://www.langorigami.com/science/computational/treemaker/treemaker.php | ||
| + | |||
| + | - A link to the Tea Bag Problem thread. | ||
| + | |||
| + | http://www.ics.uci.edu/~eppstein/junkyard/teabag.html | ||
| + | |||
| + | == Comments/Questions == | ||
| + | |||
| + | Please feel free to leave any comments or questions about this page here! | ||
== References == | == References == | ||
Aharoni, G. (2013). ''Origami swans''. Retrieved from http://www.giladorigami.com/PG_Swans.html | Aharoni, G. (2013). ''Origami swans''. Retrieved from http://www.giladorigami.com/PG_Swans.html | ||
| + | |||
| + | Aucly, D. and Cleveland, J. "Totally real origami and impossible paper folding" http://arxiv.org/pdf/math/0407174v1.pdf | ||
| + | |||
| + | CNN "The origami kayak and 9 other great folding vehicles" http://www.cnn.com/2013/10/11/tech/innovation/folding-origami-oru-kayak/ | ||
| + | |||
| + | DeMaine, E. (2010). "Folding and Unfolding" Retrieved from erikdemaine.org/folding/ | ||
| + | |||
| + | Hull, T. (2003) "Origami Geometric Constructions" http://mars.wne.edu/~thull/omfiles/geoconst.html | ||
| + | |||
| + | Lang, R. J. (2013) "Robert Lang Origami" http://www.langorigami.com/ | ||
PBS. (Nov. 30, 2009). ''Between the folds''. Retrieved from http://www.pbs.org/independentlens/between-the-folds/history.html | PBS. (Nov. 30, 2009). ''Between the folds''. Retrieved from http://www.pbs.org/independentlens/between-the-folds/history.html | ||
| Line 147: | Line 184: | ||
Serenevy, A. K. (Feb. 2003). ''Where's the math in origami? ''Retrieved from'' http://math.serenevy.net/?page=Origami-WhereMath'' | Serenevy, A. K. (Feb. 2003). ''Where's the math in origami? ''Retrieved from'' http://math.serenevy.net/?page=Origami-WhereMath'' | ||
| − | + | <br> | |
| − | + | <br> | |
| − | + | ||
| − | + | ||
[[Category:MA453Fall2013Walther]] | [[Category:MA453Fall2013Walther]] | ||
Latest revision as of 11:04, 30 November 2013
Alison Brown (brown398@purdue.edu)
Pinar Temiz (ptemiz@purdue.edu)
Contents
[hide]Origami and Mathematics
Picture from Aharoni, 2013.
Introduction/History of Origami
Origami, despite what many math believe, is orignally thought to have roots in China (PBS, 2009). This art form was brought to Japan from China. Coming from the Japanese words oru(to fold) and kami(paper)origami was only at first only available for the weathly since paper was so expensive. Since the expense was so great, oragami was mainly used for ceremonies and religious events. However, as time passed and paper was produced on a larger scale, origami became available for both the rich and poor. For the same reason, people starting creating origami for art instead of for ceremonial/religous purposes. For a long time this art form was simply passed down from one generation to the next without writing. In fact, the first written instructions were by Akisato Rito called "Thousand Crane Folding". Older forms of origami were simply paper folded to make a design such as a crane. However, modern origami is created by artists. Modern designs can even look like puzzles created by mathematicians. Akira Yoshizawa is considered one of the fathers of modern origami because he created a system of folding patterns, symbols, arrows, and diagrams to streamline this art. His methods are still being used today. Now, more and more people are creating this art using mathematical principles and ideas. The study of origami mathematics began in the 1980's (DeMaine, 2010). This field studies the properties of origami including what happens once you unfold a piece of origami. Many study the patterns and different properties the piece of unfolded paper has. A few of the "mathematical origami pioneers" include Jun Maekawa, Peter Engel, Robert Lang, and Erik Demaine. All of the mathematicians use particular constructs in order to create the amazing origami structures seen today.
Origami Mathematics
Related Mathematicians
A related Mathemetician whose work is really interesting is Robert J. Lang. He has a very good way of explaining how origami works and how we use origami in everyday life even in ways we would not have even thought. For example, he came up with an idea to get a telescope with a lens with a diameter of 100 meters, which would be the size of a football field, into space to orbit around the Earth 22,000 miles away (Lang, 2013). Lang knew that the bigger the telescope was, the better and sharper the images would be and hence he tried to make it as big as it could be with still being able to take it up into space and the idea was the it would be a thin as a sheet of paper. All space vehicles, such as heavy lift rockets, usually had a capacity to carry objects of a 4 meter diameter and that is 10 meters long. This meant that the lens had to be folded, crumpled or stuffed into the tube of the rocket. However, if there was an undesired fold then this would ruin the optical performance of the lens, therefore it had to have to be collapsed into a smaller shape by a controlled set of creases whose locations and structure would not degrade the optical performance. Robert Lang is also the developer of a computer program called TreeMaker which takes a stick figure drawing and creates a crease pattern to make the desired figure. Below, under "Examples" are the finished product of a flag, frog, and spider all created from the program TreeMaker. This program actually uses a mathematical algorithm and properties of origami figures to determine which particular creases and folds are needed in order to produce the finished piecel however, determine exactly how to fold and in what order is left to the designer. This program is interesting because Lang has even stated that the software allows him to create patterns that he would not otherwise be able to create with a pencil and paper. A link to download TreeMaker is available at the bottom of the page.
Erik DeMaine has interests in folding, or seeing how a given object such as paper can be "reconfigured or folded according to a few constraints" (DeMaine, 2010). The ultimate goal with his research is to determine an algorith for characterizing different aspects of foldability for an object or showing that no such algorithm is possible. One result in folding is something called "universal results" where in a particular model of folding, everything is possible. If "universal results" are not possible, the next best option is an "efficient algorithm" that helps determine if an object is foldable. DeMaine does not only work with origami, he has also done research in the foldings of other objects such as proteins or polyhedrons. This work is useful in the field of origami mathematics because it can help create the properties of a given piece of origami. As the field continues to develop and grow, more information will be discovered about the particular properties that make up pieces of origami.
Real Life Examples Using Mathematics and Origami
In the 1980’s origami had been used in space for a solar panel designed by Koryo Miura to fly in a Japanese satellite. There were different structures and ideas adapted for the Eyeglass telescope using origami and applying it to the telescope. They needed a radically symmetric structure and collapsed on a finite number of creases that fit within a cylindrical form factor such as a rocket. The origami structure that was settled with was called the ‘Umbrella’ as it resembled a collapsible umbrella which folded from a large flat disk down to a much smaller bordered cylinder.
How it works
Huzita's Origami Axioms
1) Given two points p1 and p2 we can fold a line connecting them.
2) Given two points p1 and p2 we can fold p1 onto p2.
3) Given two lines l1 and l2 we can fold line l1 onto l2.
4) Given a point p1 and a line l1 we can make a fold perpendicular to l1 passing through the point p1.
5) Given two points p1 and p2 and a line l1 we can make a fold that places p1 onto l1 and passes through the point p2.
6) Given two points p1 and p2 and two lines l1 and l2 we can make a fold that places p1 onto line l1 and places p2 onto line l2.
There are four natural methods to folding paper. The 1st, 2nd and 3rd methods are illustrated by figure 1 and the 4th method is illustrated by figure 2.
Which are used for this definition below:
(P,L) is an origami pair if P is a set of points in R2 and L is a collection of lines in R2 satisfying:
i) The point of intersection of any two non-parallel lines in L is a point in P.
ii) Given any two distinct points in P, there is a line in L going through them.
iii) Given any two distinct points in P, the perpendicular bisector of the line segment with given end points is a line in L.
iv) If L1 and L2 are lines in L, then the line which is equidistant from L1 and L2 is in L.
v) If L1 andL2 arelinesinL,thenthereexistsalineL3 inLsuchthatL3 isthe mirror reflection of L2 about L1.
Origami and groups are introduced in the following two definitions:
1) A subset of R2,P, is closed under origami constructions if there exists a collection of lines, L, such that (P,L) is an origami pair.
2) P0 = ∩{P | (0, 0), (0, 1) ∈ P and P is closed under origami constructions} is the set of origami constructible points.
Relation to other fields of mathematics
Origami relates in many ways to different fields of mathematics. For example, many teachers in high schools use origami to teach many topics in their curriculum. Areas included are problem solving, geometry, ratios, angles. logic, proofs, congruence, properties of parallel lines, and the list goes on. (Serenevy, 2003). One example Robert Lang gave in his TED talk was the fact that any origami figure can be unfolded and colored using only 2 colors. This would be a good example to show in a discrete mathematics class in high school (Lang, 2013). There is also a fairly obvious connection to the field of geometry. Many geometric shapes and designs can be made with one sheet of square paper using different folds. Overall, even though the mathematics is starting to have a much deeper role in the creation of origami figures, there is a practical use for this math at a high school level relating to several different mathematical fields.
Importance of Origami and Practicality of the Mathematics
Origami is used a lot in daily life and in a lot of varying things. When one generally thinks of origami, they usually think of the interesting and pretty shapes that it can create and and it has indeed been appreciated as a beautiful form of art for a very long time (there are examples of different and interesting pictures of origami below). Of course Origami has been used for many different other purposes one of which include teachers using it to teach their students about geometry and problem solving with other aspects of origami use being that of a method of therapy in all different medical fields. These include as a way to exercise hand muscles that are trying to rehabilitate and also for people who suffer from arthritis as it is seen as a good method to strengthen muscles. Also it is used in the psychology medical field and they have discovered that Origami can help with better memory, more creativity and imagination, a better attention span and even the development of their motor skills. It can also be used as a means to relieve stress also. Origami can also be used in different sciences and technology as well as art and sculptures and it is more part of our life than we may realise. Another very interesting real life use of origami is the use of transportable objects that reduce in their original size so that it is an easier way to carry them whilst you are on the move. For example in this article: http://www.cnn.com/2013/10/11/tech/innovation/folding-origami-oru-kayak/ it shows how these different methods of transport that can be folded to make it travel size. Below are the ones that we found the most interesting:
Practicality:
In all honesty, the mathematics used to create the above examples has proven extremely practical in everyday life. Having these techniques allows us to do things with objects that we were not previously able to do. For example, using mathematics to create a folding telescope that is able to be sent to space. Using the axioms listed above, the telescope was allowed to be folded into a smaller version so it was easily able to be lifted into space. While there are many practical applications of the mathematics of origami, this math would probably be incredibly difficult for students in high school to understand unless the rules were simplified. A few of the rules, or interesting facts, such as an unfolded piece of origami can be 2-colored, would be helpful for students, but much of the math is difficult to understand and explain without advanced mathematics knowledge.
While these problems are mostly mathematical, they do have a way that can relate to real life. For example, Paul Earwicker posted this question: "We buy tea in square paper bags. These are sealed around all four edges. The question is what is the maximum volume that can be contained?". Principles of origami can be used to help solve this problem, showing that that these particular properties can be useful in everyday life. A link to the problem thread is included in the "Interesting Links" at the bottom of the page.
Examples
The following are examples of origami figures as well as their crease patterns.

Flag from 1 sheet of paperCrease Pattern for the Flag above
Frog created from 1 sheet of paper
Crease pattern for the frog origami above
Spider Created from one sheet of paper
Crease pattern for spider origami above
Interesting Links
-The following is a TED Talk given by Robert Lang discussing how interesting origami figures can be constructed thanks to particular mathematical rules.
http://www.ted.com/talks/robert_lang_folds_way_new_origami.html?quote=323
- A link to download TreeMaker software by Robert Lang
http://www.langorigami.com/science/computational/treemaker/treemaker.php
- A link to the Tea Bag Problem thread.
http://www.ics.uci.edu/~eppstein/junkyard/teabag.html
Comments/Questions
Please feel free to leave any comments or questions about this page here!
References
Aharoni, G. (2013). Origami swans. Retrieved from http://www.giladorigami.com/PG_Swans.html
Aucly, D. and Cleveland, J. "Totally real origami and impossible paper folding" http://arxiv.org/pdf/math/0407174v1.pdf
CNN "The origami kayak and 9 other great folding vehicles" http://www.cnn.com/2013/10/11/tech/innovation/folding-origami-oru-kayak/
DeMaine, E. (2010). "Folding and Unfolding" Retrieved from erikdemaine.org/folding/
Hull, T. (2003) "Origami Geometric Constructions" http://mars.wne.edu/~thull/omfiles/geoconst.html
Lang, R. J. (2013) "Robert Lang Origami" http://www.langorigami.com/
PBS. (Nov. 30, 2009). Between the folds. Retrieved from http://www.pbs.org/independentlens/between-the-folds/history.html
Serenevy, A. K. (Feb. 2003). Where's the math in origami? Retrieved from http://math.serenevy.net/?page=Origami-WhereMath