| (One intermediate revision by the same user not shown) | |||
| Line 13: | Line 13: | ||
Find the constant c such that <math class="inline">f_{\mathbf{XY}}(x,y)</math> is a valid pdf. | Find the constant c such that <math class="inline">f_{\mathbf{XY}}(x,y)</math> is a valid pdf. | ||
| − | [[Image:002. | + | [[Image:002.png]] |
<math class="inline">\iint_{\mathbf{R}^{2}}f_{\mathbf{XY}}\left(x,y\right)=c\cdot \text{Area}=1</math> where <math class="inline">\text{Area}=\frac{1}{2}.</math> | <math class="inline">\iint_{\mathbf{R}^{2}}f_{\mathbf{XY}}\left(x,y\right)=c\cdot \text{Area}=1</math> where <math class="inline">\text{Area}=\frac{1}{2}.</math> | ||
| Line 40: | Line 40: | ||
<math class="inline">\hat{y}_{MAP}\left(x\right)=\arg\max_{y}\left\{ f_{Y}\left(y|\left\{ \mathbf{X}=x\right\} \right)\right\}</math> but <math class="inline">f_{Y}\left(y|\left\{ \mathbf{X}=x\right\} \right)=\frac{1}{1-x}\cdot\mathbf{1}_{\left[0,1-x\right]}\left(y\right)</math> . Any <math class="inline">\hat{y}\in\left[0,1-x\right]</math> is a MAP estimator. The MAP estimator is NOT unique. | <math class="inline">\hat{y}_{MAP}\left(x\right)=\arg\max_{y}\left\{ f_{Y}\left(y|\left\{ \mathbf{X}=x\right\} \right)\right\}</math> but <math class="inline">f_{Y}\left(y|\left\{ \mathbf{X}=x\right\} \right)=\frac{1}{1-x}\cdot\mathbf{1}_{\left[0,1-x\right]}\left(y\right)</math> . Any <math class="inline">\hat{y}\in\left[0,1-x\right]</math> is a MAP estimator. The MAP estimator is NOT unique. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
---- | ---- | ||
Latest revision as of 11:47, 3 December 2010
Example. Two jointly distributed random variables
Two joinly distributed random variables $ \mathbf{X} $ and $ \mathbf{Y} $ have joint pdf
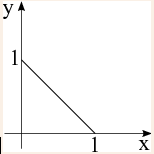
$ f_{\mathbf{XY}}\left(x,y\right)=\begin{cases} \begin{array}{ll} c ,\text{ for }x\geq0,y\geq0,\textrm{ and }x+y\leq1\\ 0 ,\text{ elsewhere.} \end{array}\end{cases} $
(a)
Find the constant c such that $ f_{\mathbf{XY}}(x,y) $ is a valid pdf.
$ \iint_{\mathbf{R}^{2}}f_{\mathbf{XY}}\left(x,y\right)=c\cdot \text{Area}=1 $ where $ \text{Area}=\frac{1}{2}. $
$ \therefore c=2 $
(b)
Find the conditional density of $ \mathbf{Y} $ conditioned on $ \mathbf{X}=x $ .
$ f_{\mathbf{Y}}\left(y|\left\{ \mathbf{X}=x\right\} \right)=\frac{f_{\mathbf{XY}}\left(x,y\right)}{f_{\mathbf{X}}(x)}. $
$ f_{\mathbf{X}}(x)=\int_{-\infty}^{\infty}f_{\mathbf{XY}}\left(x,y\right)dy=\int_{0}^{1-x}2dy=2\left(1-x\right)\cdot\mathbf{1}_{\left[0,1\right]}(x). $
$ f_{\mathbf{Y}}\left(y|\left\{ \mathbf{X}=x\right\} \right)=\frac{f_{\mathbf{XY}}\left(x,y\right)}{f_{\mathbf{X}}(x)}=\frac{2}{2\left(1-x\right)}=\frac{1}{1-x}\textrm{ where }0\leq y\leq1-x\Longrightarrow\frac{1}{1-x}\cdot\mathbf{1}_{\left[0,1-x\right]}\left(y\right). $
(c)
Find the minimum mean-square error estimator $ \hat{y}_{MMS}\left(x\right) $ of $ \mathbf{Y} $ given that $ \mathbf{X}=x $ .
$ \hat{y}_{MMS}\left(x\right)=E\left[\mathbf{Y}|\left\{ \mathbf{X}=x\right\} \right]=\int_{\mathbf{R}}yf_{\mathbf{Y}}\left(y|\left\{ \mathbf{X}=x\right\} \right)dy=\int_{0}^{1-x}\frac{y}{1-x}dy=\frac{y^{2}}{2\left(1-x\right)}\biggl|_{0}^{1-x}=\frac{1-x}{2}. $
(d)
Find a maximum aposteriori probability estimator.
$ \hat{y}_{MAP}\left(x\right)=\arg\max_{y}\left\{ f_{Y}\left(y|\left\{ \mathbf{X}=x\right\} \right)\right\} $ but $ f_{Y}\left(y|\left\{ \mathbf{X}=x\right\} \right)=\frac{1}{1-x}\cdot\mathbf{1}_{\left[0,1-x\right]}\left(y\right) $ . Any $ \hat{y}\in\left[0,1-x\right] $ is a MAP estimator. The MAP estimator is NOT unique.