| (3 intermediate revisions by the same user not shown) | |||
| Line 10: | Line 10: | ||
Note how much more exciting <math>sin(t)-cos(2t)</math> is than <math>sin(t)</math>. Here the sampling frequency is very small, on the order of <math>10^4</math> | Note how much more exciting <math>sin(t)-cos(2t)</math> is than <math>sin(t)</math>. Here the sampling frequency is very small, on the order of <math>10^4</math> | ||
| − | [[Image: | + | [[Image:HW2A2a_ECE301Fall2008mboutin.jpg]] |
* [[Matlab Code _ECE301Fall2008mboutin]] | * [[Matlab Code _ECE301Fall2008mboutin]] | ||
| − | [[Image: | + | |
| − | * [[Matlab | + | Here we have increased the sampling frequency to pi/2, making it appear like a periodic DT function. Note that pi/2 is still a multiple of the inverse of the fundamental period. |
| + | |||
| + | [[Image:HW2A3a_ECE301Fall2008mboutin.jpg]] | ||
| + | * [[Matlab Code _ECE301Fall2008mboutin]] | ||
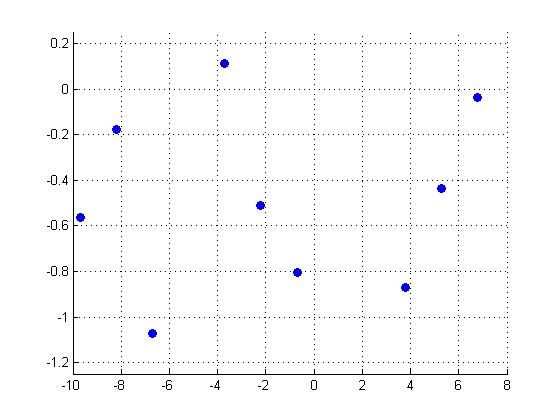
| + | Here is an example of what happens when we use an inverse of the fundamental period as our sampling frequency. Our beautiful, exciting <math>sin(t)-cos(2t)</math> function has been reduced to little more than a random assortment of dots. | ||
Latest revision as of 15:10, 12 September 2008
Part A: Periodic Signals Revisited...Periodic Signals Revisited...Periodic Signals Revisited
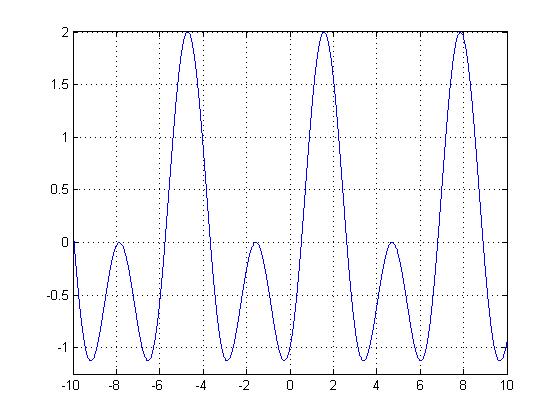
As we discussed in class, a function $ x(t) $ is periodic if $ x(t+T)= x(t) $ , where T is a multiple of the fundamental period, or smallest period.
In the first homework, I explained how $ sin(t) $ was periodic. However, because that is rather boring, let's take a look at $ sin(t)-cos(2t) $.
Note how much more exciting $ sin(t)-cos(2t) $ is than $ sin(t) $. Here the sampling frequency is very small, on the order of $ 10^4 $
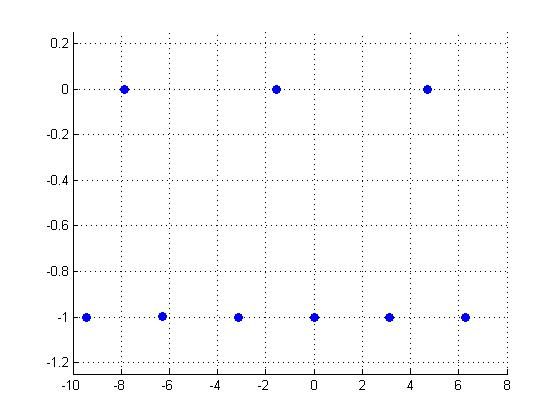
Here we have increased the sampling frequency to pi/2, making it appear like a periodic DT function. Note that pi/2 is still a multiple of the inverse of the fundamental period.
Here is an example of what happens when we use an inverse of the fundamental period as our sampling frequency. Our beautiful, exciting $ sin(t)-cos(2t) $ function has been reduced to little more than a random assortment of dots.