The Graph Isomorphism Problem
Group A: Luis Baeza, Grayson Ricketts, Nicholas Baribeau, Nicolas Bratton, Qinxin Shi
Contents
[hide]Introduction
The graph isomorphism problem has been a long-standing problem in complexity theory for the last four decades. The statement of the problem is fairly simple: Given any two finite graphs that may appear to be different, is there an "easy" way to tell whether or not the two graphs are the same? We'll look at the statement of the problem in a slightly more rigorous setting, discuss the importance of the problem in other fields, as well as some recent progress made on the problem by a professor at the University of Chicago.
The problem of graph isomorphism is mostly examined from a computability perspective. It has not been shown to be NP-Complete nor P and has alluded classification for decades. Although no classification has been discovered, there are algorithms for general graphs and special types of graphs to determine isomorphisms.
The graph isomorphism problem have many applications and are used across many disciplines.
Basic concepts
We'll start off with some basic concepts related to the problem and formulate a more rigorous statement of the problem.
$ \ \text{Definitions} $
• A $ \ \text{Graph } G $ is a pair of sets $ \ G = (E_{G}, V_{G}) $ , where $ \ V_{G} $ is the set of vertices (or "dots") in the graph and $ \ E_{G} $ is the set of edges (or "lines") for the graph.
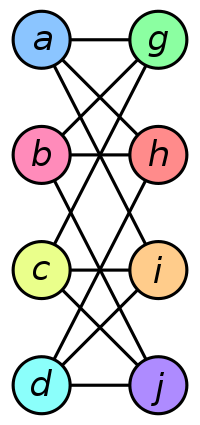
• A $ \ \text{Graph Isomorphism } f $ between two graphs $ \ G \text{ and } H $ is a bijective function $ \ f : V_{G} \rightarrow V_{H} $ with the property that there is an edge between $ \ v_{i} \text{ , } v_{j} \in V_{G} $ if and only if there is an edge between $ \ f(v_{i}) \text{ , } f(v_{j}) \in V_{H} $ . In other words, this is a one-one correspondence between $ \ G \text{ and } H $ showing that they are in fact the same graph. One example of a graph isomorphism is the following:
| Graph A | Graph B | $ \ f : V_{A} \rightarrow V_{B} $ |
|---|---|---|
 |
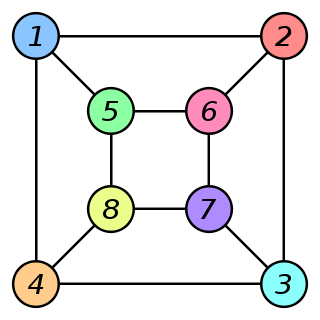 |
$ f(a) = 1 $ $ f(b) = 6 $ |
Using the information in the table above, we can essentially rearrange Graph A to make Graph B by relabeling vertices and moving them around accordingly. Observe that even for the two graphs with only eight vertices, it is not obvious that there is an isomorphism between them. However, note that given a function defined like the one above, it is easy (for a computer) to check if it is in fact an isomorphism between the two graphs. Thus the Graph Isomorphism Problem is an NP Problem.
One can ask if there are algorithms for determining such an isomorphism $ f $ given any two graphs. One such way to tackle the problem is to go through each possible way a vertex can be mapped to another vertex by brute-force; This method is outlined in the Algorithm section. As discussed below, this method is not efficient for determining an isomorphism between two graphs.
This leads us to wonder about the existence of more efficient algorithms to determine an isomorphism for two seemingly distinct graphs. In essence, the Graph Isomorphism Problem is to determine the optimal time complexity of an algorithm which finds a desired isomorphism between two graphs. In other words, what is the running time (polynomial time (P), exponential time, etc.) of the most optimal algorithm which solves this problem? As stated before, the answer to this question has remained unsolved for decades.
Applications
Isomorphic graphs have a lot of applications nowadays. All the entities in the world can be represented by some sort of connections. A big part of today's technology is to figure out these connections and relations. Every time when we show an isomorphism between such relations with graphs, a new star starts to shine on the firmament of human thinking power.
Listed below are some of the more concrete areas that use graph isomorphism:
- In automata theory. There are multiple uses. The main one is to show that some two languages are equal.
- In parallel processing: to reason about behavior of complex systems.
- In verification of things: e.g. computer programs, logic proofs, or even electronic circuits.
- In compilers. e.g. perform optimizations.
- In search engines that use formulas more sophisticated than words. e.g. in biology DNA structures.
- Security. e.g. fingerprints scanners, facial scanners, and retina scanners.
- Civil engineering, city planning, building interior planning (e.g. recognizing geographic locations with desired properties).
- Analysis of social structures (special cases may include schools, military, parties, events, etc.).
- Analysis of business relations.
- Any system that performs clustering would benefit from fast graph-isomorphism algorithm, e.g.
- linking two Facebook accounts of the same person
- recognizing web users based on their behavior
- recognizing plagiarism in students solutions
Time Complexity
The graph isomorphism problem is in NP. However, it has not been proven it is in NP-complete and a polynomial time algorithm has not been found. Many believe that the problem lies somewhere in between NP-Complete and P, although this has not been proven.
If the graph isomorphism problem was shown to be in NP but not in P nor NP-Complete it would automatically prove P is not equal to NP.
In 2015, László Babai from the University of Chicago presented an algorithm that has a quasi-polynomial time. If this finding is verified, the quasi-polynomial time would make the graph isomorphism much closer to P than NP-Complete, but still not in P. Babai himself speculated that the problem was very close to the boundary for the class P but not inside.
Algorithm
Given two graphs A and B, in order for them to be isomorphic, every node in graph A must have a corresponding node in graph B such that given an edge between two nodes in graph A, there must be an edge between the corresponding nodes in graph B, and vice versa. The simplest way to demonstrate isomorphism between two graphs would be to construct a list of corresponding nodes. One method for constructing this list would be to use adjacency matrices. Given that graphs A and B have n nodes, the following steps should show whether or not they are isomorphic:
- Label the nodes of graph A as 1 through n and construct an adjacency matrix for A.
- Label the nodes of graph B as 1 through n and construct an adjacency matrix for B.
- Compare the adjacency matrices for A and B. If they are identical, A and B are isomorphic. If they are not, go back to step 2, labeling the nodes differently.
- If all the possible numberings of graph B have been exhausted and no match has been found, A and B are not isometric.
While this method might work well for small graphs, this method quickly takes unmanageably long to compute as the size of graphs A and B increase. Specifically, any brute force method such as this one takes (at most) n! comparisons. Although this algorithm will consistently return the correct answer, for practical reasons it is unusable.
For several special cases (mentioned below) it is possible to determine the isomorphism of a graph more efficiently than by using a brute-force, factorial runtime algorithm. However, no general algorithm exists yet that can determine isomorphism between two graphs in polynomial time.
History
The history of math in general is one of those subjects that while interesting to some people is incredibly dull for others so to discuss the history of graph isomorphism allow me to skip over thousands of years where humans muddled through with just numbers and shapes and bring you to 1736 where everybody’s favorite mathematician, Euler, published a paper called Seven Bridges of Königsberg. This paper is widely regarded as the first to begin to delve into the idea of graphs. It related formula to the number of vertices and edges of a given graph. Another paper published near the same time discussing a similar topic was produced by Vandermonde called The Knight Problem. These papers were studied and generalized by Cauchy and L’Huillier. More than 100 years later Cayley would add a paper to this group about trees which are a specific type of graph. Cayley linked his findings to the work of Pólya in the 1930’s which was then generalized by De Bruijn in 1959. After this beginning to graph theory came about the idea of isomorphism was added to it and we have the problem we have today. Now a days, many questions about graph isomorphism are solved much more easily thanks to the wonderful advent of powerful computers. Through this method many questions about graph isomorphism have been answered but it would not be mathematics if one answer didn’t raise ten more.
Special Cases
A problem one often runs into with graph isomorphisms is what to do when a graph is labeled, it is easy enough to see if an unlabeled graph is isomorphic to another unlabeled graph but in order to deal with graphs that have labels or weights or both one must come up with a slightly altered definition of an isomorphism. Two main altered definitions have been proposed the first is that “an isomorphism is a vertex bijection which is both edge preserving and label preserving” this is a rather strict definition that would allow only graphs with the exact same edges and labels and structure to map to each other. The second definition is somewhat similar stating “an isomorphism is an edge-preserving vertex bijection which preserves equivalence classes of labels”. Due to the first and second definitions’ strictness, many mathematicians embrace these definitions as only variations on the original definition where structure is the highest priority. Some special cases for graph isomorphisms are listed below:
Trees
A tree is an undirected graph in which there are no vertices are connected by more or less than one edge. Due to the simplicity of this graph in comparison to other graphs there are quite a few numbers of vertices that have been solved meaning that given a number of vertices, how many isomorphisms are there for an unlabeled tree. The sequence of which can be found here: [1]. While this is not an inclusive sequence, it is quite a long one and may be the longest we have for isomorphisms of special cases.
Planar Graphs
A planar graph is another special graph where it may be represented in a plane and the edges do not intersect except at the end points. This is a special case because as long as one has infinite time, it is possible with our current grasp on the graph isomorphism problem to determine the amount of isomorphic graphs for any finite number of vertices.
Other
Many other special cases of graphs have been solved in terms of isomorphism some of these are interval graphs, permutation graphs, and bounded-parameter graphs.
References
Dtldarek, “applications of the isomorphic graphs” from Discrete Mathematics, Retrieved April 20, 2016, from http://math.stackexchange.com/questions/120408/what-are-the-applications-of-the-isomorphic-graphs
Klarreich, Erica. "Landmark Algorithm Breaks 30-Year Impasse" Quanta Magazine. 14 Dec. 2015. Web. 20 Apr. 2016.
McKay, B., & Piperno, A. “Practical Graph Isomorphism” 17 April 2016. Retrieved from http://pallini.di.uniroma1.it/Introduction.html
Neapolitan, Richard E., Kumarss Naimipour, and Richard E. Neapolitan. Foundations of Algorithms. Sudbury, MA: Jones and Bartlett, 2011. Print.
Weisstein, Eric W. "Isomorphic Graphs." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/IsomorphicGraphs.html
"Graph Isomorphism" Wikipedia: The Free Encyclopedia. Wikimedia Foundation, Inc. 22 July 2015. Web. 20 Apr. 2016.
Chartrand, Gary, Linda Lesniak, and Ping Zhang. Graphs & Digraphs. Boca Raton: Chapman & Hall, 2011.Print.

