The Mathematics of Scheduling
Scheduling is arranging or planning events to occur at a certain time. It serves as an answer to questions such as "How long does it take to build a house?" The answer to this simple question is actually quite complicated due to the many factors that must be considered. For instance, there are obvious factors, such as the size of the house, or the materials needed; however, there are more complicated factors, like coordinating people and equipment to accomplish the goal in a timely way. This leads to the study of Combinatorial Scheduling.
Basic Definitions
•Processors- These are the "workers" that will complete the tasks
•Tasks - This is an indivisible unit of work
•Processing Time - The time needed for a processor to complete a given task, X
Basic Assumptions
For simplicity, we assume the following three assumptions
•Versatility - Any processor can execute an task
•Uniformity - The processing time for a task is the same regardless of which processor is executing the task
•Perseverance - Once a processor starts a task, it will complete the task without interruption
Precedence Relations
If you cannot complete a task Y, without first completing a task X, (X→Y) this is referred to as a Precedence Relation
However, two tasks are said to be Independent if neither X nor Y have a precedence relation.
(AcyclicDigraphs)
Another note about precedence relations is that they exhibit transitivity. If (X→Y) and (Y→Z), then (X→Z).
(ex1comb)
Lastly, we cannot have a set of precedence relations that form a cycle. In other words, we cannot have (X→Y) and (Y→Z) and (Z→X).
More Terminology
•Project-A set of tasks to be completed
•Finishing Time - The duration of the project from the start of the first task to the completion of the last task
•Optimal Schedule- A schedule with the minimum project finishing time or has the optimal finishing time
A note about the optimal finishing time is that the optimal finishing time for any project is the minimum sum of time of the precedence relationships. For example, given tasks W, X, Y, and Z and an infinite number of processors, and if Y cannot be completed before X, but W, X, and Z are independent, then the minimum finishing time is the combined time of X and Y.
•Directed Graphs (Digraphs)
Digraphs serve as a way to represent asymmetric relationships (i.e. X related to Y does not imply Y is related to X)
The following terminology apply to digraphs:
•Arcs- Similar to edges, every arc is described by its starting vertex and ending vertex. Thus XY describes X→Y, but does not apply to Y→X
•Arc-set- This is a list of all arcs in a digraph. For example digraph A = {XY, YX}
•Incident to/from- If XY is an arc in the digraph, X is incident to Y, similarly Y is incident from X
•Adjacent- If the starting point of YZ is the ending point of XY, then YZ is adjacent. In other words, one can go from X to Z by way of Y
•Path- The sequence of arcs from one vertex to another. For example a path from vertex X to vertex W could consist of a sequence of arcs XY,YZ,ZU...., VW.
•Cycle- When a path starts and ends on the same vertex
•Outdegree/Indegree- The outdegree of vertex X is the number of arcs with X as their starting point, likewise the indexer of vertex X is the number of arcs with X as their ending point.
Below are examples of digraphs:
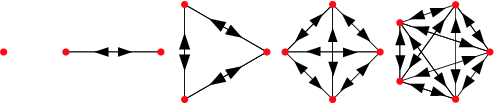(completeDigraph)
Priority Lists
A list of all the tasks prioritized in the order we prefer to execute them is a priority list.
The number of priority lists in a project consisting of M tasks is M! = M X (M-1) X .... X 2 X 1
Scheduling Algorithms
Decreasing-Time Algorithm - This algorithm creates a priority list based on decreasing time. For example, given WX(8), XY(2), and YZ(4) (where the time for each task is given by the numbers in the parenthesis), then the decreasing-time priority list is WX,YZ,XY. The problem with this algorithm is that it is "greedy." In other words, it does not account for precedence relationships, and only prioritizes things in the movement of decisions.
Critical Paths Algorithm - If there is a long set of tasks that need to be completed in order, then this algorithm accounts for this, and places higher priority on tasks that precede a larger set of tasks. Before the algorithm, some definitions and another algorithm must be defined.
•For a given vertex X of a project digraph, the critical path for X is the path from X to END with the longest processing time (the sum of all processing times along this path). When we add the processing times of all the tasks along the critical path for a vertex X, we get a Critical time for X
•The path with the longest processing time from START to END is called the critical path for the project, and the total processing time for this critical path is called the critical time for the project.
Backflow Algorithm- The backflow algorithm is used to find critical paths. The steps are as follows:
Step 1: Find the critical time for every vertex of the project digraph. This is done by starting at END and working backward toward Start according to the this rule: the critical time for a task X equals the processing time of X plus the largest critical time among the vertices incident from X.
Step 2: Once we have the critical time for every vertex in the project digraph, critical paths are found by just following the path along largest critical times.
These are the steps for the Critical Paths Algorithm:
Step 1: Use the back flow algorithm to find the critical time for every task in the project
Step 2: Using the critical times in Step 1, create a priority list with the tasks listed in decreasing order of critical times
Step 3: Using the priority list obtained in Step 2, create the schedule.
Final Notes
A final note on the Decreasing-Time Algorithm and the Critical Paths Algorithm is that neither is guaranteed to give the optimal finishing time. However, these algorithms give a close to optimal finishing time, and are useful for scheduling any project.
References
AcyclicDigraphs,retrived from "mathworld.wolfram.com/images/eps-gif/AcyclicDigraphs_800.gif"
ex1comb, retrived from "dot2tex.readthedocs.org/en/latest/_images/ex1comb.png"
retrived from "graphs.grevian.org/resources/static/images/example3.png"
retrived from upload.wikimedia.org/wikipedia/commons/thumb/a/a2/Directed.svg/250px-Directed.svg.png
CompleteDigraph retrived from mathworld.wolfram.com/images/eps-gif/CompleteDigraphs_901.gif
retrived from www.sitmo.com/wp-content/uploads/2015/11/example4.png
