Penrose Tiling
By Joshua John Clark, Daniel Kerstiens, Jason Piercy, and Caleb Rouleau
Outline:
Overview of Penrose Tiling Example: 
Artist: Urs Schmid Photo by: Urs Schmid Date: drawn in 1995
Who is Roger Penrose?
Sir Roger Penrose started out his career at the University of Cambridge. He obtained his Ph.D. there in algebraic geometry in 1957. He is famous not only for Penrose tiling, but also for work with Stephen Hawking to show that a black hole is a singularity where all mass in the black hole is compressed into a single point with infinite density and zero volume. He was knighted in 1994. [14]
Penrose continues to do research in physics and mathematics. He wrote two books, Emperor’s New Mind (1989) and Shadows of the Mind (1994), on how quantum mechanics can be used to explain how the brain works. The recent 2010 book Cycles of Time: An Extraordinary New View of the Universe describes the idea that the Big Bang recurs endlessly. [14]
Penrose tiling existed before Penrose, but Penrose did extensive research over it in the 1970s. [15]
Definition of non-periodic
Periodic function are those which repeat their values at regular intervals. One example of this is the sin function. In contrast, non-periodic functions do not repeat their values.
Similarly, periodic tilings form some kind of repeated pattern, but non-periodic tilings have no repeated pattern. [16]
For more information, please see https://www.projectrhea.org/rhea/index.php/HW1.4_Ben_Laskowski_-_Periodic_and_Non-Periodic_Functions_ECE301Fall2008mboutin or https://www.projectrhea.org/rhea/index.php/HW1.4_Steve_Anderson_-_Examples_of_Periodic_and_Non-Periodic_ECE301Fall2008mboutin
Types of Penrose Tilings
1. Original Pentagonal
"Penrose's first tiling uses pentagons and three other shapes: a five-pointed "star" (a pentagram), a "boat" (roughly 3/5 of a star) and a "diamond" (a thin rhombus."[12]
The tiles are laid out based on rules to force non-periodicity. The following link shows the original Penrose tiling.
[1]
2. Kite and Dart
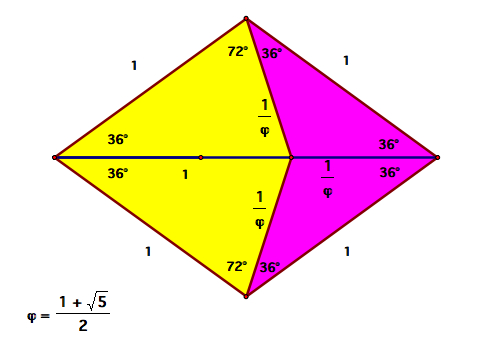
Kite and dart tiles were created by dividing a rhombus as shown below. Phi is the golden ratio. A pentagon is constructed with the kite and dart an arranged in a non-periodic tiling. They
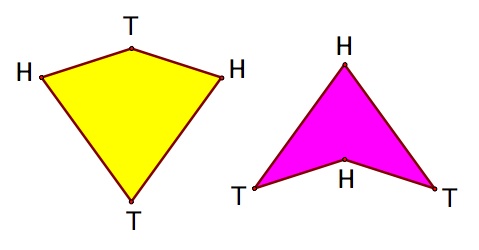
are arranged using rules developed by Penrose and John Horton Conway, both mathematicians at Princeton. The second image below shows how the the kite and dart are laid out. The H and T
vertices can only touch vertices of the same type.[11] The images below show the kite and dart and a tile layout using this method.
3. Rhombus
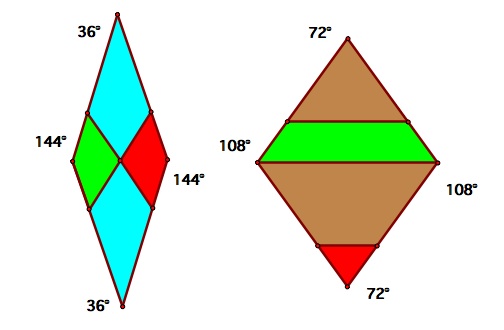
Another method of Penrose tiling uses fat and thin rhombi formed from the pentagons. Once again, mathematical rules connect the rhombi to force non-periodicity. "In this case, the red tabs
may only touch other red tabs and the green tabs only touch other green tabs."[11]
Symmetry
Penrose Tilings have two different types of symmetry: reflectional and rotational. The tiling's style of symmetry overall is referred to as local pentagonal symmetry[1], which means that patterns appear to repeat in small sections of the tiling. As these tilings are non-periodic, however, they do not have translational symmetry.
A Penrose tiling can't have more than one point of global five-fold symmetry. The reason for this fact is that rotating about an extra point of global five-fold symmetry would generate two closer centers of five-fold symmetry, which causes a contradiction with a lack of translational symmetry[2].
Also, the golden ratio (1 + sqrt(5)) / 2 appears within several aspects of Penrose tilings, some noted below[3].
Rules for construction
So how does one construct a Penrose tiling? The first thing to do is to pick the set of basic tiles from which to construct the tiling. Sir Roger Penrose originally came up with a set of 6 tiles, and later realized that he could simplify the set to only two tiles. The most common set is a pair of rhombi of the same side length, one with acute angle 36 degrees, and the other with acute angle 72 degrees. Note that each angle of the two rhombi is some multiple of 36 degrees, which is 180/5 degrees. This is where the 5-fold symmetry originates. There are other sets of tiles that work as well, such as the kite-and-dart that are made from dividing a rhombus with acute angle 72 degrees. [4]
These sets of tiles can be used to form periodic patterns as well as the aperiodic patterns of Penrose tiling, so there needs to be a set of matching rules to make sure that one obtains a Penrose tiling. These matching rules are related to how the sets of tiles were discovered in the first place.
Penrose used substitution tiling to discover the small sets of two tiles. Substitution tiling is the practice of replacing one tile with smaller tiles to create a new pattern. A regular pentagon could be divided into 6 smaller regular pentagons, with some space between them. Each of those 6 pentagons can be divided further into 6 smaller pentagons. Then, the gaps between those pentagons are filled in with rhombi, stars, or “paper boat” shapes. (See [5] or [6]). So, the pentagon was incompletely substituted for using these new shapes. Each of these new shapes can then be substituted for by using two rhombi, or by using a kite and a dart. So, a 5-fold aperiodic pattern was developed by using small, simple shapes of tiles to substitute for a large pentagon.
These tiles have to be put together in specific ways to be able to substitute for the small pentagons, rhombi, stars, and “paper boats” that substitute for the large pentagon. Out of observations of this fact came “matching rules” for putting the tiles together to form Penrose tilings.
For example, take the set of tiles containing two rhombi. Take the rhombus of acute angle 36 degrees and label on of the 144 degree angles. Label the opposite sides with arrows pointing toward the opposite vertex. Then label one of the 72 degree angles and draw arrows on the opposite sides pointing away from the opposite vertex (See [7]). Then make an infinite number of copies and arrange them so that labeled angles only touch labeled angles and adjacent sides either have no arrows or have arrows pointing the same way. Following these rules ensures that you get a tiling with 5-fold symmetry. And all tilings with 5-fold symmetry must be aperiodic.[5]
This leads to an interesting fact: only 8 combinations of the two rhombi can be used to form any intersection, and these 8 combinations make it so that the ratio of “thick” to “thin” rhombi is the golden ratio.[7] Certain ways of putting the rhombi together also correspond to projecting a 5-dimensional integer lattice onto a plane.[8]
Applications of Penrose Tiling
Penrose tiling has a surprising number of applications, mainly due to the fact that it has some order (5-fold symmetry, local symmetries) but is aperiodic overall. Some metals have 5-fold symmetry in their diffraction patterns.[4],[7] These materials are classified as “quasicrystals” because their crystal lattices are not periodic, but instead resemble a form of Penrose tiling. This feature makes them resistant to wear, and they make good coatings for non-scratch surfaces.[7] Penrose also used Penrose tilings to create puzzling board games with Pentaplex[7], and he sued Kleenex in 1997 over copyright infringement from using Penrose tiling patterns to create “thicker and softer” toilet paper that doesn’t “bunch up” because of its aperiodicity.[7],[9] This has prompted debate over the legitimacy of patenting mathematical discoveries.[10]
Other tilings
Johannes Kepler developed some early tiling methods by treating star polygons as regular polygons. However, Kepler's tilings were not aperiodic.[13] The following link shows an example of a Kepler tiling. [2]
References
[1] Austin, David (2005), "Penrose Tiles Talk Across Miles", Feature Column (Providence: American Mathematical Society).
[2] Gardner, Martin (1997), Penrose Tiles to Trapdoor Ciphers, Cambridge University Press, ISBN 978-0-88385-521-8.
[3] Grünbaum, Branko; Shephard, G. C. (1987), Tilings and Patterns, New York: W. H. Freeman, ISBN 0-7167-1193-1. Gallian, J. (2013).
[4] Rusin, Dave. http://www.math.niu.edu/~rusin/known-math/94/penrose.alg
[5] Kaplan, Craig. "The Trouble with Five." http://plus.maths.org/content/os/issue45/features/kaplan/index
[6] Penrose, Roger. "Pentaplexity: A Case of Non-Periodic Tilings of the Plane." The Mathematical Intelligencer 1998, Vol. 2, Iss. 1, pp. 32-37.
[7] Boyle, Allison. "From quasicrystals to Kleenex." http://plus.maths.org/content/os/issue16/features/penrose/index
[8] Olbrich, Dave. "Penrose Tiles." http://traipse.com/penrose_tiles/index.html
[9] "Penrose Tiling vs. Kleenex." http://docs.law.gwu.edu/facweb/claw/penrose.htm
[10] Morris, Carl. "Penrose’s Patent and the Battle of the Tissue Tiles (Contains Mathematics)." http://quixoticquisling.com/2009/01/penroses-patent-and-the-battle-of-the-tissue-tiles-contains-mathematics/
[11] Schultz, Kyle. "Penrose Tilings." http://jwilson.coe.uga.edu/emat6680fa05/schultz/penrose/
[12] http://en.wikipedia.org/wiki/Penrose_tiling
[13] Dutch, Steven. "Penrose Tilings." http://www.uwgb.edu/dutchs/symmetry/penrose.htm
[14] http://www.britannica.com/EBchecked/topic/450252/Sir-Roger-Penrose
[15] http://en.wikipedia.org/wiki/Penrose_tiling
[16] http://en.wikipedia.org/wiki/Non-periodic
Contemporary abstract algebra. (8th ed.). Boston, MA: Brooks/Cole, Cengage Learning.
![[1]](http://en.wikipedia.org/wiki/File:Penrose_Tiling_(P1).svg){kind=link}
![[2]](http://www.uwgb.edu/dutchs/Graphics-Other/TILINGS/kepler0.gif){kind=link}