Generalizing Kuratowski's Theorem: Drawing Graphs on a Doughnut
By: Mihai Avram, Frank Lagoe, Theresa Kaufmann, Xin Li, and Cory Smith.
If you try to draw K_5 in the plane (or on a sphere) you will not be able to do it without crossing edges. Explain how on a doughnut K_5 and even K_6 can be drawn. Is K_7 possible? What about other surfaces such as a pretzel?
Introduction:
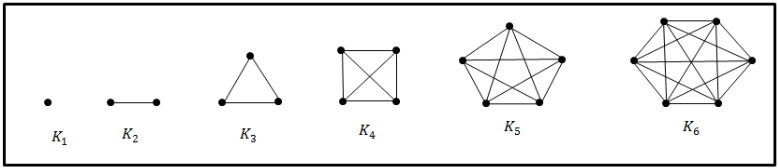
K_n graphs are an important concept in Graph Theory, but before we talk about K_n graphs we must elaborate on what a simple graph is. A simple graph is defined as a graph in which each edge connects a pair of distinct vertices and no two edges should connect the same pair of vertices. Each K_n group of graphs is a simple graph and is defined as a complete graph (each vertex is connected to all the other vertices) on n vertices. We can see some examples of K_n graphs below:
A question that once riddled Mathematicians was whether the K_5, K_6, and K_7 graphs were possible to draw on a plane, sphere, doughnut, or pretzel without crossing edges. In this report we use Euler’s Theorem stating that if a graph G is planar and connected, and if one chooses any plane representation, then (vertices of G) - (edges of G) + (faces of G) = 2, and Graph Theory and Kuratowski's Theorem to answer some of these questions. This formula V-E+F will equal two for the Sphere and the Pretzel and will equal zero for the Doughnut.
Kuratowski's Theorem states that a finite graph is planar if and only if it does not subsume a subgraph which is a subdivision of K_5 or K_3,3.
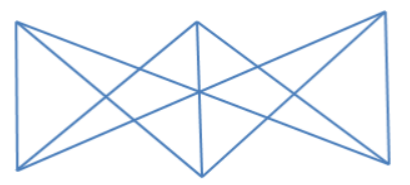
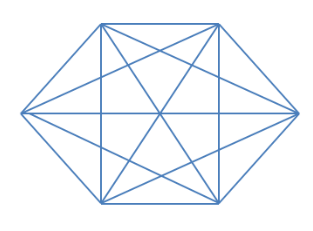
An image of K_3,3 is shown below:
Theory:
Euler's formula can be used to derive a minimum value for the genus of a graph such that a complete graph can be embedded on a surface.
Another theorem derived from Euler’s formula states that “If a graph G has genus g, then G can be drawn without edge-crossing on every surface Sn for which n≥g, Therefore the value determined for previously is a minimum number that the graph of Kn can be embedded on.
Using the formula for lower bound of the genus we find that both K_5, and K_6 require a graph of at least S1. By our second derivative of Euler’s formula, any higher value graph will also allow for the embedding of K_5, and K_6. The pretzel surface is of form S2, therefore both K_5, and K_6 can be placed on to the pretzel surface, without any crossings. Illustrations are provided below:
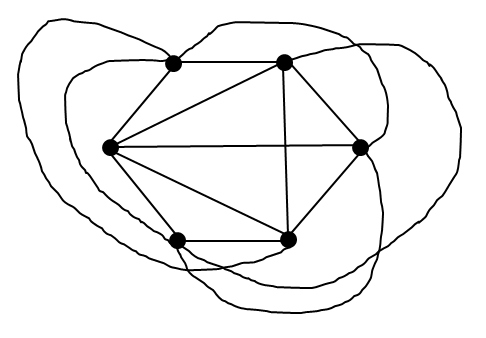
Can a K_5 graph be planar in a Doughnut?
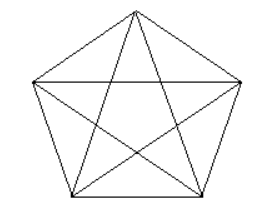
K_5 Graph:
K_5 in a plane: not possible to be planar → edges cross
Relating back to the Euler formulas:
v + f - e = 2 - 2g
5 + f - 10 = f - 5 = 2 - 2g --> 2g = 7 - f.
Since g is an integer, f must be an odd number. We can also see from the picture above that 6 ≥ f ≥ 4. Hence f = 5, and
2g = 7 - 5 = 2 --> g = 1
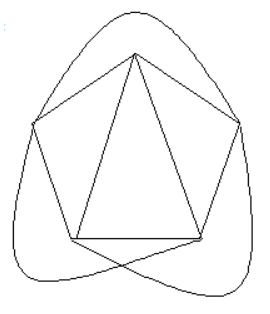
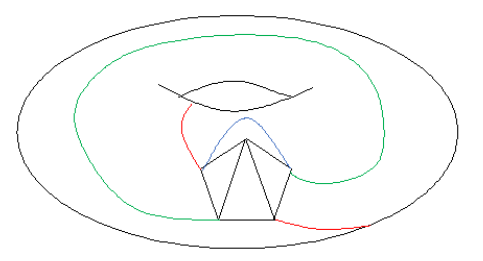
So by Euler's Theorem, K_5 can be drawn without lines crossing on a surface S_1 (a doughnut). This is visualized below:
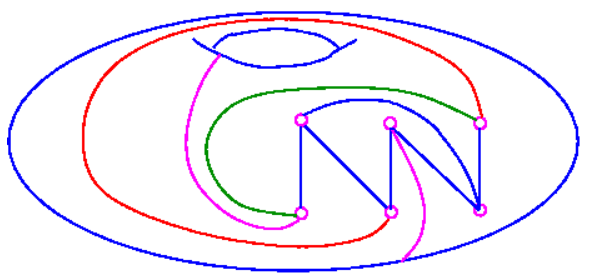
Can a K_6 graph be planar in a Doughnut?
K_6 graph:
K_6 in a plane: Not possible to be planar because K_5 is a subgraph of K_6 and K_5 is not planar.
Relating back to the Euler formulas, we can try to show that K_6 can be drawn on S_1. Since K_5 is a subgraph of K_6, the number of faces of K_6 when drawn on the same surface as K_5 must be greater than 5. It can also be no greater than the number of faces of K_5 drawn on a donus plus 5 since 6 new faces would describe a planar K_6 on S_0 since g is minimal. We already know this to be impossible. Hence,
5 < f < 11 and
f = 2 + e - 2g - v = 2 + 15 - 6 - 2g = 11 - 2g
--> 2g = 11 - f
Since g is minimal, we use g = 1 to describe K_6 on a doughnut. Below, it is shown that K_6 is a planar graph with 9 faces on S_1.
Can a K_5 graph be planar in a Pretzel?
Yes, this 3D model of a pretzel and the Theory section shows that it can be done.
Can a K_6 graph be planar in a Pretzel?
Yes, this 3D model of a pretzel and the Theory section shows that it can be done.
Are K_7 planar graphs possible to draw on a Pretzel or Doughnut?
For the complete graph of K_7 we find that the minimum Sn that it can be embedded on is S1, and so K_7 can occur on both the pretzel, and the doughnut. This is the highest order graph that may occur on on the doughnut however, this is the highest order complete graph that can be drawn on the donut. K_8 may be drawn on the pretzel, however K_9 requires a higher order surface.
References:
Rashid Bin Muhammad's Home Page. (n.d.). Rashid Bin Muhammad's Home Page. Retrieved April 27, 2014, from http://www.personal.kent.edu/~rmuhamma/GraphTheory/graphTheory.htm
Rosen, K. H. (2012). 10. Discrete Mathematics and its Applications (7th ed., ). Boston: WCB/McGraw-Hill.