Use of Fourier Transforms in MP3 Audio Compression
MP3, or more precisely MPEG-1 Audio Layer 3,is part of an audio-visual standard called MPEG.
Why MPEG-1 Layer-3?
- Open standard: The specification is available to everybody interested in implementing the standard. - Availability of encoders and decoders and other supporting technologies
Basic Concept behind MP3 Compression
With MP3, the sound samples are transformed using methods that involve Fourier Series Transformations. A frequency analysis of the sound is the basis for this transformation. Based on this frequency analysis, the sound is split into frequency bands, each band corresponding to a particular frequency range. With MP3, 32 frequency bands are used. Based on the frequency analysis, the encoder uses what is called a psycho-acoustic model to compute the significance of each band for the human perception of the sound. The idea is that the the human ear can only discern sounds from 20Hz to 20KHz, so any data outside of this threshold can be discarded to make the file smaller.
The information remaining after frequency analysis and using a psycho-acoustic model is coded efficiently with (a variant of) Huffman coding. MP3 supports bit rates from 32 to 320 kb/s and the sampling rates 32, 44.1, and 48 kHz. The format also supports variable bit rates (the bit rate varies in different parts of the file). An MP3 encoder also stores metadata about the sound, such as the title of the audio piece, album and artist name and other relevant data.
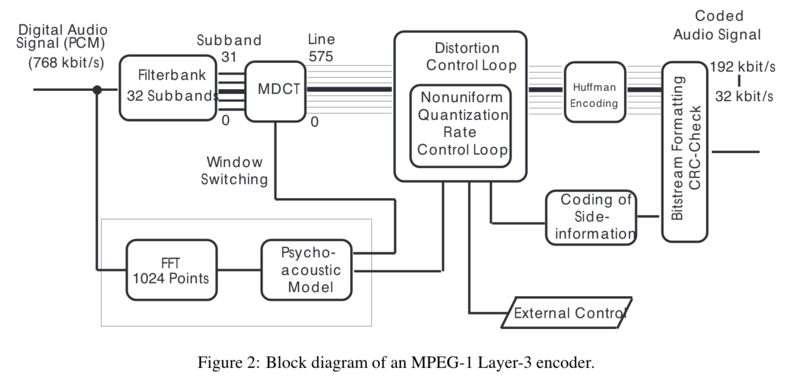
Given blow is a block diagram of MPEG-1 Layer-3 encoder.
The overall algorithm is broken up into 4 main parts.
● Part 1 divides the audio signal into smaller pieces, these are called frames. An MDCT filter is then performed on the output.
● Part 2 passes the sample into a 1024-point FFT, and then the psychoacoustic model is applied. Another MDCT filter is performed on the output.
● Part 3 quantifies and encodes each sample. This is also known as noise allocation. The noise allocation adjusts itself in order to meet the bit rate and sound masking requirements.
● Part 4 formats the bitstream, called an audio frame. An audio frame is made up of 4 parts, The Header, Error Check, Audio Data, and Ancillary Data.
PART 1: MCDT (Modified Discrete Cosine Transform) FILTER
The MDCT is a Fourier related transform based on type-IV DCT. It has an additional property of being “lapped.” This linear function transforms 2N real numbers to N real numbers according to the equation:
$ F:R^{2N} → R^N $
$ X_{k} = \sum_{n=-\infty}^{2N-1}x_{n}\cos{\frac{\pi}{N}(n+\frac{1}{2}+\frac{N}{2})(k + \frac{1}{2})} $
The MDCT limits the sources of output distortion at the quantization stage. It is also used as and analysis filter given by:
$ h_{k}(n) = w(n)\sqrt{\frac{2}{M}}\cos[{\frac{(2n+M+1)(2k+1)(\pi)}{4M}}] $
The MDCT performs a series of inner products between the input data x(n), and the analysis filter hk(n). This eliminates the blocking artifacts that would cause a problem during the reconstruction of the sample. The final signal is given by:
$ x(n) = \sum_{k=0}^{M-1}[X(k)h_{k}(n) + X^{P}(k)h_{k}(n+M)] $
PART 2: 1024-point FFT (Fast Fourier Transform)
The FFT is an algorithm that computes the Discrete Fourier Transform and its inverse. In general the DFT is found by using the equation:
$ X_{k} = \sum_{n=0}^{N-1}x_{n}e^{-2i{\pi}k\frac{n}{N}} $ Where $ X_{0}...X_{N-1} $are complex numbers and k = 0... N-1
The FFT is used as a filter bank on an audio sample. It is used to filter out unwanted or unneeded data from the sample.
● First, incoming audio samples, s(n) , are normalized based the following equation x(n):
$ x(n) = \frac{s(n)}{N(2^{b-1})} $
Where N is the FFT length of the sample and b is the number of bits in the sample.
● Second, the masking threshold of the sample is found by using an estimate of the power density spectrum, P(k). P(k) is computed by using a 1024-point FFT.
$ x(n) = P_{k} + 10{\log}[\sum_{n=0}^{N-1}h(n)x(n)exp(-j{\frac{2{\pi}kn}{N}})]^2 $, 0 ≤ k ≤ N-1
Where h(n) is a Hann Window
References:
[1] //www.math.utah.edu/~gustafso/s2012/2270/web-projects/Guckert-audio-compression-svd-mdct-MP3.pdf [2] //http://www.linkwitzlab.com/Brandenburg_mp3_aac.pdf