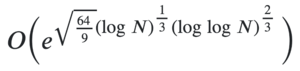Contents
[hide]Cryptography in Classical, Quantum and Post-Quantum Realms
Mathematical breakthroughs in the realms of cryptography and the ethical challenges they pose
INTRODUCTION
Imagine yourself waking up to a regular day a couple of years from now when you rise from bed and find your phone flooding with alert notifications: all your bank accounts and investment portfolios have been breached and emptied, your emails and social media accounts have been infiltrated, and all your personal information was leaked. You find out that it’s not just you, this is happening to everyone around the world. Chaos and panic break loose. How could this have happened!?
While this is an extreme example, the situation is certainly possible. For decades, we’ve been using the same encryption and decryption methods, such as RSA, DES, and ECDSA, to protect our data. These cryptographic1 protocols and algorithms, though now they seem clever and highly useful, are mainly dependent on the complexity of the factorization of the product of large prime numbers, which is sufficient to guard against the computing power that an attacker may have access to today, but poses a vulnerability3 when quantum computers enter the picture.
This is where a distinction appears between three different realms of Cryptography: Classical, Quantum2, and Post-Quantum. Classical or Conventional Cryptography is what we use extensively today. It relies on the computational difficulty of mathematical problems to protect data from non-quantum threats. Differently, Quantum Cryptography attempts to exploit the properties of quantum mechanics, rather than difficult math problems, to protect data from quantum threats. Finally, Post-Quantum Cryptography also relies on mathematical problems, but they’re much more complex than the ones in classical cryptography and can withstand quantum attacks. Post-Quantum assumes a situation in the future in which it is conventional for any personal computer to have quantum power and everyone can have access to it.
Now that we’ve defined some common understanding on this subject, we can envision how a situation like the one described at the beginning of this introduction could happen, and why the early development and improvement of Quantum and Post-Quantum cryptographic techniques are crucial to keep up with the research and development in quantum computing and avoid a catastrophic susceptibility.
Cryptography has widely been used as a means of information security in today’s electronic world, and its demand will only increase as we face new technologies and more and more of our personal lives and information is stored digitally. However, the increased reliance on cryptographic methods can raise several ethical questions of global concern that are closely related to fundamental human rights like privacy, inequality of access, intellectual property, and copyright issues. In this project, we are going to discuss different breakthroughs in the three separate realms of cryptography, summarize the theory and mathematics behind them, and explain not only how they are effective and the security advancements they bring, but also what new liabilities they could expose and ethical challenges that they raise.
RSA
What is RSA, how does it work, what are its vulnerabilities?
So what exactly is RSA encryption? RSA, or Rivest-Shamir-Adleman, its creators, is "a public-key cryptosystem that allows us to encrypt messages between two communicating parties so that an eavesdropper who overhears the encrypted messages will not be able to decode them" (Cormen). A public-key cryptosystem also allows for a party to send a digital signature along with their message. This signature loses its validity if any bit of the message is changed which provides authentication of both the message and the sender. This makes RSA encryption the perfect tool for authenticating any electronic communications.
Each party in a public-key cryptosystem has both a public key and a secret key. In the RSA public-key cryptosystem, a party creates his or her public and secret keys as follows:
- Select at random two large prime numbers p and q such that $ p ≠ q $.
- Compute $ n = pq $.
- Select a small odd integer e that is relatively prime to $ λ(n) $.
- $ λ(n) $ is the Carmichael function which is the smallest positive integer m such that $ a^m≡1\ \ \ (mod\ n) $ holds for every integer a coprime to n.
- Coprime means that the two numbers share no common divisors except for 1.
- For RSA encryption, n is always the product of two prime numbers, p and q, so $ λ(n) = lcm((p-1),(q-1)) $.
- Compute d as the multiplicative inverse of e modulo $ λ(n) $.
- $ d ≡ e^{-1}\ \ \ (mod\ λ(n)) $
- $ de ≡ 1\ \ \ (mod\ λ(n)) $
- Publish the pair $ P=(e,n) $ as the public key.
- Keep secret the pair $ S=(d,n) $ as the secret key.
Traditionally, when talking about two parties sending encrypted messages, Bob and Alice are the standard names for the sender and receiver. If Bob wants to send an encrypted message to Alice, he will have to obtain Alice's public key. Once he has done so, Bob can sent a message M to Alice. To do this, Bob will have to convert his message to an integer m, such that $ 0≤m<n $. He then computes the ciphertext c, using Alice's public key:
- $ \begin{align} c(m)=m^e\ mod\ n \end{align} $
Upon receiving Bob's encrypted message, Alice and decrypt the message using her private key and the decryption function:
- $ \begin{align} m(c)=c^d\ mod\ n \end{align} $
Why does taking the cyphertext to the power of d decrypt it? The way we calculated d means that there exists an integer k such that $ de = kλ(n)+1 $
- $ \begin{align} c^d ≡ m^{ed} ≡ m^{kλ(n)+1} ≡ m^{kλ(n)} * m ≡ (m^{λ(n)})^k * m ≡ 1^k * m ≡ m\ \ \ (mod\ n) \end{align} $
The security of RSA relies on the difficulty of factoring n. The task of performing an RSA private key decryption given only the public key is known as the RSA problem. The most efficient method known to solve the RSA problem is by factoring the modulus n, which is believed to be impractical when n is sufficiently large ($ n>=1024 $ bits. The RSA key setup routine already turns the public exponent e, with this prime factorization, into the private exponent d, and so exactly the same algorithm allows anyone who factors n to obtain the private key. Any ciphertext c can then be decrypted. Factoring n however, is unlikely without the use of quantum computers.
The Quantum Threat to RSA Security: Shor's Factoring Algorithm
Peter Shor's discovery in 1994 of a quantum algorithm that finds the prime factors of an integer in an amount of time that only grows as a polynomial with the size of the integer opened up fundamentally new possibilities for cryptography. Most importantly, it showed it was possible to combine the parallelism inherent in quantum states with useful theorems from number theory to produce a serious threat to the security of systems based on RSA, since RSA assumes that factoring can never be carried out in polynomial time. All known classical factoring algorithms do not break this computational "speed limit," but Shor's algorithm shows that this security assumption is not valid in a world with fully functional quantum computers.
To describe Shor's algorithm, we need three concepts. First, we need to define what quantum states are mathematically. Second, we need to see how quantum states give probabilities for different outcomes via the Born rule. Third, we need to describe how interacting qubits are modeled by a mathematical object known as the tensor product.
Quantum States
Fortunately, we can set aside questions about how to picture quantum states with our intuitions molded by the classical world, and instead give a definition in terms of vector spaces. A quantum state is a vector with complex number entries, and a quantum state space is a vector space spanned by linear combinations of specific vectors chosen to represent mutually exclusive outcomes of an experiment. These vectors are called basis states, since every other member of the larger quantum state space can be expressed as a linear combination of them using complex numbers. So, a quantum state Q can be expressed as $ Q=z_1B_1+z_2B_2+...+z_nB_n $, where $ \{B_1,...,B_n\} $ is a basis for the state space and $ z_1,..., z_n $ are complex numbers.
Many applications involve finite-dimensional quantum state spaces, and Shor's algorithm falls under this category since the quantum portion of it uses qubits. A qubit is the quantum analog of the classical bit formed by linear combinations of the basis states $ 0 $ and $ 1 $, so a qubit is a $ 2 $-dimensional state space. This already suggests that it might be worthwhile to look for ways to process information with a quantum rather than a classical computer since a bit only has $ 2 $ possible states, $ 0 $ or $ 1 $, whereas a qubit has as many possible states as there are complex numbers, so continuously many.
The Born Rule: From Complex Numbers to Probabilities
These definitions can't be the whole story, since actually interacting with a qubit only ever produces a $ 0 $ or a $ 1 $ with some probability, never a "fuzzy" version of these possible values. We need the Born rule to bridge the gap between a quantum state and the chances of what actually occurs in the world.
The Born rule states that the probability of seeing an outcome associated with a basis state is the product of the complex coefficient of that basis state with its complex conjugate. The complex conjugate of a complex number $ a+ib $ is $ a-ib $. Geometrically, this corresponds to reflecting the first complex number over the real axis in the complex plane to reach the second. So, for a qubit $ QB=z_1(0)+z_2(1) $, where $ z_1=a+ib $, the probability of seeing the outcome 1 is $ (a+ib)(a-ib) $. (Just as with classical bits, we don't need to end up with a number on a dial; all that's required is that the events named "0" and "1" be mutually exclusive, like a device being turned on or off.)
It might look as if the Born rule comes out of nowhere, but in the context of the vector definition of quantum states, it makes sense for finding probabilities, which can never be negative and have to sum to 1. For the first property, the Born rule makes sure that negative probabilities never arise because multiplying a complex number by its complex conjugate always gives a non-negative real number, which we can see by algebra:
$ (a+ib)(a-ib)=a^2-iab+iab-i^2b^2=a^2-(-1)b^2=a^2+b^2 $.
This leads directly into the second property since the magnitude of a complex number is the length of the vector from the origin to that number in the complex plane: $ \| a+ib \| = \sqrt{a^2+b^2} $. This means that $ a^2+b^2=\| a+ib \|^2 $, and for all of the complex coefficients of the basis states, it must be the case that $ \| z_1 \|^2 + \| z_2 \|^2+...+\| z_n \|^2=1 $. This corresponds to the requirement that the probabilities of a set of mutually exclusive and exhaustive events sum to 1. To return to a qubit, $ z_1(0)+z_2(1) $, this means that it must be the case that $ \| z_1 \|^2+\| z_2 \|^2=1 $. This is always possible to set up since we can divide the entries of a quantum state vector by its length to give a vector of length 1.
Tensor Products: Combining Vector Spaces
Now we can describe how the interacting qubits Shor's algorithm uses are modeled mathematically. It's clear that a qubit is a 2-dimensional vector space, but it's less clear how the vector space of multiple qubits should look, since there isn't a straightforward picture for motivation as there is in the classical domain. The use of what are known as tensor products gives the most natural way to describe multiple qubits.
A tensor product is a vector space formed from two or more other vector spaces using basis vectors from each one to make new basis vectors for the new space. So, if $ QB_1 $ and $ QB_2 $ are qubits, both with the basis $ \{ 0,1 \} $, then the combined quantum state space $ QB_1QB_2 $ is a vector space spanned by the four new basis states $ {(00),(01),(10),(11)} $, so the new vector space is 4-dimensional. Just as with a single qubit, the states in this new system of two qubits are linear combinations of these 4 basis states using complex numbers: $ z_1(00)+z_2(01)+ z_3(10)+z_4(11) $. For larger systems of $ n $ qubits, the dimension of their tensor product becomes $ 2^n $.
This exponential increase in the dimension of the vector space of interacting qubits corresponds to how much more information quantum systems can store compared to classical ones, and it's the main source of the speedup Shor's algorithm offers over known classical factoring algorithms.
Shor's Algorithm: Leveraging the Dimension of Tensor Products Through Number Theory
Now we have the basic components we need to describe Shor's algorithm. Fundamentally, the power of Shor's algorithm comes from combining the exponential amount of information that a system of qubits can process with tools from number theory to arrive at a way to circumvent the exponential increase in difficulty for known classical algorithms to factor larger and larger integers. There are two parts to the algorithm that correspond to these conceptual ingredients. First, the algorithm converts the problem of factoring an integer to an equivalent problem of finding a period in a sequence of numbers, and second, the algorithm manipulates multiple qubits to actually find the period. This provides the factors of N since the first step already showed that the problems are equivalent, so, to solve one is to solve the other.
For the first part, the algorithm takes $ N $, the integer to be factored that's odd and not a power of a prime number, then randomly chooses another integer $ K $ such that $ 1<K<N $, and computes the greatest common divisor of $ K $ and $ N $. The strict inequalities are to make sure that only divisors not equal to $ 1 $ or $ N $ show up in further steps. Both the random choice of $ K $ and the use of quantum randomness in the second part make Shor's algorithm probabilistic, so actually implementing it, even on a large and functional quantum computer, would require running it multiple times to increase the chances of getting the right answer. Fortunately, $ \text{gcd}(K,N) $ is easy for classical computers to find even for larger numbers thanks to the Euclidean algorithm. This step also checks whether the second quantum part is necessary, since if $ \text{gcd}(K,N)=M \neq 1 $, then $ M $ is already a proper divisor of $ N $, that is, a divisor not equal to $ 1 $ or $ N $. The quantum part of Shor's algorithm comes in for the case where $ K $ and $ N $ don't have any factors in common other than $ 1 $, so $ \text{gcd}(K,N)=1 $.
Moving from the problem of factoring an integer to the problem of finding a period in a sequence of integers is possible because of the properties of modular arithmetic. If $ A,B, $ and $ C $ are integers, $ A $ is congruent to $ B $ modulo $ C $ if $ C $ divides the difference $ A-B $. In symbols, $ A \equiv B(\text{mod }C) $. For example, $ 9 \equiv 3(\text{mod }6) $ since the difference $ 9-3=6 $ is divisible by $ 6 $. $ A \equiv B(\text{mod }C) $ is equivalent to $ B $ being the remainder after dividing $ A $ by $ C $, so $ 9 \equiv 3(\text{mod }6) $ since dividing $ 9 $ by $ 6 $ leaves remainder $ 3 $.
Choosing a modulus allows for making a sequence of integers that must be periodic with a period no greater than the modulus. For example, choosing $ 2 $ as the modulus and considering the sequence $ 1,2,3,4,5,6,7... $ gives the sequence $ 1,0,1,0,1,0,1,... $ because every integer is either even or odd, which is equivalent to either leaving no remainder after division by $ 2 $, or leaving remainder $ 1 $. So, this sequence has period $ 2 $, which meets the condition of being no greater than the chosen modulus.
This feature of modular sequences comes into Shor's algorithm through the next stage, setting up the function $ f(E)=K^E(\text{mod }N) $, where $ K $ is the integer randomly chosen at the beginning such that $ 1<K <N $, $ N $ is the integer to be factored, and the exponent $ E $ runs through the natural numbers. Just like the binary sequence for the modulus $ 2 $, the sequence of remainders of powers of $ K $ to the modulus $ N $ must be periodic, though as $ N $ grows, the period will become about as hard to find in a classical setting as finding prime factors.
Setting up this function $ f(E) $ is relevant to finding the factors of $ N $ because of what must be true if $ \text{gcd}(K,N)=1 $. If the sequence repeats after $ J $ numbers, and the period $ J $ is even, then it must be the case that $ K^J \equiv 1(\text{mod }N) $ since $ N $ is odd, which becomes $ K^J-1 \equiv 0(\text{mod }N) $. Since the number on the left is a difference of squares, this becomes $ (\sqrt{K^J}+1)(\sqrt{K^J}-1) \equiv 0(\text{mod }N) $. But this means that the number on the left leaves no remainder when divided by $ N $. This is equivalent to it being a multiple of $ N $, so it must include all of the prime factors of $ N $. (Making sure the period $ J $ is even makes sure that the number on the left is still an integer, since taking the square root divides the exponent $ J $ by $ 2 $, and allows for rewriting the difference of squares.)
It follows that finding $ \text{gcd}(\sqrt{K^J}-1,N) $ and $ \text{gcd}(\sqrt{K^J}+1,N) $ must end in finding a factor of $ N $ that's not equal to $ 1 $ in at least one case. This fact guarantees that finding the period $ J $ leads to finding the factors of $ N $, and if the random choice of $ K $ at the beginning results in a period that's not even, the algorithm can start over with a different choice for $ K $.
The second part of Shor's algorithm uses the power of multiple qubits to actually find the period $ J $ that's the key to finding the factors of $ N $. This is possible because the tensor product of the qubits has a high enough dimension to allow for setting up a correspondence between the possible factors of $ N $ and the basis states of the tensor product. Converting the integers from $ 1 $ to $ N-1 $ to binary results in a list of sequences of 0 and 1, each of which can then become one of the basis states. Manipulating the combined system of qubits allows for processing every possible form of the function $ f(E) $, bypassing the need to evaluate only one at a time. This level of parallelism is not available on a classical computer, and relies on the exponential growth of the dimension of the tensor product. Applying the Born rule to the combined system to get information about the period out inevitably destroys some information, but this doesn't pose an insurmountable problem since the algorithm can start again and use more and more runs to shave down the chances that it arrives at the wrong answer, or only gives the number $ N $ rather than one its proper factors. The number of qubits needed to represent the possible factors in binary grows as $ N $ gets larger, but the resulting complexity is still much better than the exponential growth in difficulty for classical algorithms. Specifically, the number of quantum operations required is bounded above by $ cL^2(\text{log}_2L)(\text{log}_2\text{log}_2L) $, where $ c $ is a constant and $ L $ is the length of $ N $ after it's converted to binary.
Ethical Implications: The Tension Between Freedom of Inquiry and National Security
The implications of Shor's algorithm are significant not just for cryptography, but also for the tension between letting researchers pursue and publish any ideas they like, and the need to maintain national security and the integrity of the many systems that depend on bad actors having no way to factor huge integers in polynomial time. Since the project of building large, error-correcting quantum computers is ongoing, with billions of dollars poured into this effort by the US government in 2022 on top of the National Quantum Initiative begun in 2018, a lot is at stake in developing quantum computers. The situation is similar to the development of nuclear technology in the 1940s, where the fundamentals of the science involved are known around the world, but governments treat specific applications with the highest secrecy. Since Shor's algorithm is, at this point in time, still waiting for large quantum computers to be built to run it on very large numbers, it's still rational to assume that RSA is secure. So, no government will completely alter their security systems, but this assumption depends on no other governments possessing a quantum computer able to process enough qubits to factor the huge numbers applications of RSA use. On one hand, research depends on international cooperation, the successful detection of quantum entanglement between a satellite and a device on Earth's surface in 2017 being just one example, but on the other hand, every government with the money and the researchers to pursue building larger quantum computers has strong incentives to do so, since cracking RSA would give them access to the most sensitive communications and information of other governments. What Peter Shor's discovery makes clear is that the future of mathematical and scientific research is not possible to predict with certainty, and that governments must walk a thin line between allowing free and open research, and staying one step ahead of potential bad actors who could exploit new knowledge.
Lattice Cryptography
Within the next few decades, we are unlikely to see quantum computing become viable for anyone besides well-funded governments and organizations. Benefits and risks are unlikely to majorly affect the public, but risks remain for people in power as well as systems like cryptocurrency, which is still a multi trillion dollar industry.
Currently, the record number of q-bits sits at 433 by IBM’s Osperey which costs about $15 million. Applying Moore’s Law for cost, we get 1.5x10^7 / 2^(28 years / 2) ~ $915. This means we should plan to see quantum computing become highly integrated in the next 30 years but will likely see major advancements in the next 15-20.
Taking a look at the speedup that quantum computing would bring to RSA cracking, we turn to the runtime expression for the General Number Field Sieve, the best known classical algorithm for factoring extremely large numbers, which is sub exponential but super polynomial.
Currently RSA encryption takes 1024-2048 bit numbers. Generally RSA numbers are approximately 1448 bits long.
Evaluating for 2^1448 we get:
~ 1.2033 * 10^24
Comparing this to shors algorithm with a runtime of:
O(log^3(n)) with log base 2 approximation we get:
~ 3.03 * 10^9.
Comparing these two values, we get an improvement of
~ 3.03 * 10^14 times
Modern QM gates take on the order of 200 nanoseconds to “switch”, while modern silicon transistors take about 100 picoseconds to switch. Taking into consideration this difference we get a real speedup of ~ 1.515 * 10 ^ 11 times.
This still puts RSA encryption as unbreakable in the age of the universe to unbreakable in many thousands of years. However, with the speedup of quantum gates, as well as faster algorithms, it is likely blockchain will face numerous quantum attacks in the near future.
Therefore, much work has been put into creating quantum-resistant cryptography algorithms. Currently, lattice based encryption seems to be the most fruitful, as it is straightforward to implement, optimized for current classical hardware which often performs matrix multiplications as well as integer multiplication, and does not have a currently known quantum algorithm that gives a significant speedup.
Lattice Encryption is based on the fact that the simple linear algebra function
Ax=b
Is actually a one way attack resistant function, and
Ax+e=b
Is even more resistant.
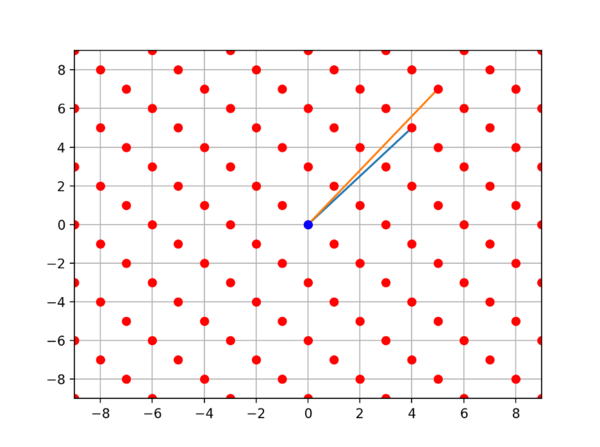
Looking at an example problem, we define a lattice L as all integer linear combinations of the basis vectors (4, 5) and (5, 7). That lattice will look like so:
Lattices are generally defined as all integer linear combinations of integer basis vectors:
$ L=A_{mn}x_n $ where $ A_{ij} ∈ Z $ and $ x_n $ is the set of $ Z^n $
Since the angle between our vectors is small, it is very difficult to go backwards and find the closest points to some vector (x0, y0). This would be the same as finding
Ax~e where A is the concatenation of (4, 5) and (5, 7), and where x and e are column vectors. The use of ~ is asking to find a solution that is in the lattice that is closest to the vector e.
Given e = (4, -3)
This means we are solving the linear system of equations 4a+5b=4
5a+7b=-3
Solving for a and b we get
a = 43/3
b = -32/3
Using these values we get the closest possible integer combination of
14 and -11
These map to the point
14 * (4, 5) + -11 * (5, 7) = (56, 70) – (55, 77) = (1, -7)
This is not at all close to (4, -3), and the two possible closest linear combinations are
16 * (4, 5) + -12 * (5, 7) = (4, -4)
12 * (4, 5) + -9 * (5, 7) = (3, -3)
Classically, there is no way to solve this problem in under exponential time and there currently exists no quantum algorithm with a greater than exponential speed up like Shor’s algorithm. Though getting the correct answer in this case was trivial, an example with a lattice matrix of size 10,000 x 10,000 would prove exponentially much more challenging, and actually cannot be solved trivially at the moment. In the future however, new algorithms to solve lattice encryption may be found. It seems to be the ethical choice for researchers to continue work on QM in regards to breaking these cryptographic algorithms, as quantum techniques can also be used for good to create truly unbreakable encryption. Halting research would allow bad actors to move ahead of current infrastructure, opening up new vulnerabilities that aren't ready to be solved.
-- Footnotes --
1 Cryptography: refers to the technique used to ensure the integrity, and authenticity of data when passing secret information securely between two parties in a public environment where unauthorized users and malicious attackers may be present so that only intended receivers can decrypt it.
2 Quantum: A quantum is the smallest discrete unit of a phenomenon. Quantum computing is an area of computer science that uses the principles of quantum theory, which explains the behavior of energy and material on the atomic and subatomic levels. Quantum computing uses subatomic particles, such as electrons or photons. Quantum bits, or qubits, allow these particles to exist in more than one state (i.e., 1 and 0) at the same time.
3 Researchers have proved that modern cryptographic algorithms such as RSA are breakable using quantum computers in polynomial time complexity.
References
Aaronson, S. (2013). Quantum computing since Democritus. Cambridge University Press.
Bernstein, D.J. (2009). Introduction to post-quantum cryptography. In: Bernstein, D.J., Buchmann, J., Dahmen, E. (eds) Post-Quantum Cryptography. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-88702-7_1
Classical vs. Quantum vs. Post-Quantum Cryptography. Quantropi. (2022, October 27). Retrieved from https://www.quantropi.com/differences-between-classical-quantum-post-quantum-cryptography/#:~:text=Classical%20cryptography%20uses%20difficult%20mathematical,and%20can%20withstand%20quantum%20attacks.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to algorithms (3rd ed.). MIT Press.
Cucurull, J. (2022, May 17). Cryptography: Conventional, Quantum, Post-Quantum. Medium. Retrieved from: https://medium.com/edge-elections/cryptography-conventional-quantum-post-quantum-9f7f4ec84732
de Wolf, R. (2017, September 15). The potential impact of quantum computers on society - ethics and information technology. SpringerLink. Retrieved from: https://link.springer.com/article/10.1007/s10676-017-9439-z
Evans, Z. (2020). Quantum Ethics. Thetechbrook.com. Retrieved from: https://thetechbrook.com/quantum-ethics/
Frankenfield, J. (2022, September 21). Quantum Computing: Definition, how it's used, and example. Investopedia. Retrieved from https://www.investopedia.com/terms/q/quantum-computing.asp
HPC. (2022, August 9). Researchers develop world's fastest two-qubit gate between two single atoms. HPCwire
Jordan, T. F. (1986). Quantum mechanics in simple matrix form. Dover Publications.
Loepp, S. & Wootters, W. K. (2006). Protecting information: From classical error correction to quantum cryptography. Cambridge University Press.
Manin, Y. I. & Zilber, B. (2010). A course in mathematical logic for mathematicians (2nd ed.). Springer.
Mavroeidis, V., Vishi, K., Zych, M. D., & Jøsang, A. (2018). The Impact of Quantum Computing on Present Cryptography. International Journal of Advanced Computer Science and Applications, 9(3). Retrieved from https://arxiv.org/pdf/1804.00200.pdf.
Pal, O., Jain, M., Murthy, B. and Thakur, V. (2022). Quantum and Post-Quantum Cryptography. In Cyber Security and Digital Forensics (eds M.M. Ghonge, S. Pramanik, R. Mangrulkar and D.-N. Le). https://doi.org/10.1002/9781119795667.ch2
Parmar, P.N. (2019) Classical Cryptography and Quantum Cryptography. GeeksForGeeks.org. Retrieved from: https://www.geeksforgeeks.org/classical-cryptography-and-quantum-cryptography/amp/
Van Leeuwen, B. (2020, July 11). Number field sieve with provable complexity. arXiv.org. Retrieved from https://arxiv.org/abs/2007.02689
Weisstein, E.W. Number Field Sieve. MathWorld--A Wolfram Web Resource. Retrieved from: https://mathworld.wolfram.com/NumberFieldSieve.html