Special sequences of numbers
Student project for MA375.
In this page, I am going to talk about one special sequence of numbers called Fibonacci sequence and its application.
You guys must be familiar with sequences from a few past class lectures. However, before starting my topic, I would like to briefly discuss it. A sequence of numbers is a set of numbers with an order (unlike in a set, order really matters in a sequence!). Another trait, which differ sequence with set, is that one number may appear more than once in a sequence. A sequence can be infinite or finite depends on the number inside is infinite or finite. Most sequences we are dealing with in math class have rules, so we can find the value of elements in the sequences.
That’s enough definitions for sequence; let’s get start on the special kind of sequence, Fibonacci sequence.
In 1202, Fibonacci introduced this sequence on his bookLiber Abaci. If you want to know more about him, here is a link described his life story:en.wikipedia.org/wiki/Fibonacci
The first two numbers in the Fibonacci sequence are 0,1. The next number is by adding the former two numbers and keep doing it for later numbers. (for example, the third number is 0+1=1; the forth number is 1+1=2; the fifth number is 1+2=3...)
The rule for Fibonacci sequence would be xn=xn-1+xn-2
(Here is a list of numbers in Fibonacci sequence:
0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946,17711,...)
A very classic example of Fibonacci question would be the "rabbit problem". (Fibonacci mentioned it in Liber Abaci in 1202.)
Putting a pair of two new born rabbits(one male and one femal) in a wild, their mate age is one month and it took female rabbit one mouth to give a birth. Assume rabbits never die and the female rabbits always produce two rabbits with different gender. How many rabbits will exist after one year?
| month |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
... |
12 |
| new |
1 |
0 |
1 |
1 |
2 |
3 |
5 |
... |
89 |
| mature |
0 |
1 |
1 |
2 |
3 |
5 |
8 |
... |
144 |
| total |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
... |
233 |
number of new pair rabbits= number of the previous mature pair rabbits(because every pair of mature rabbits would produce one new pair
number of mature pair rabbits= number of the previous new pair rabbits + # of the previous mature pair rabbits.
number of total rabbits= number of current new pair rabbits + # of current mature pair rabbits.
It is obviously too see that those three rows are having the same formula for their sequence: xn=xn-1+xn-2
Another example would be the climbing stairs: There are 10 steps in one stair, you can only climb one or two at one time. How many different ways you can use to reach the top?
| 1 step | 1 | |
|
|
|
| 2 steps | 1+1 | 2 | |
|
|
| 3 steps | 1+1+1 | 2+1 | 1+2 | |
|
| 4 steps | 1+1+1+1 | 2+1+1 | 1+2+1 | 1+1+2 | 2+2 |
| ... | ... | ... | ... | ... | ... |
You will also found Fibonacci in this case. So there are 89 different kinds of ways to reach the 10th stair.
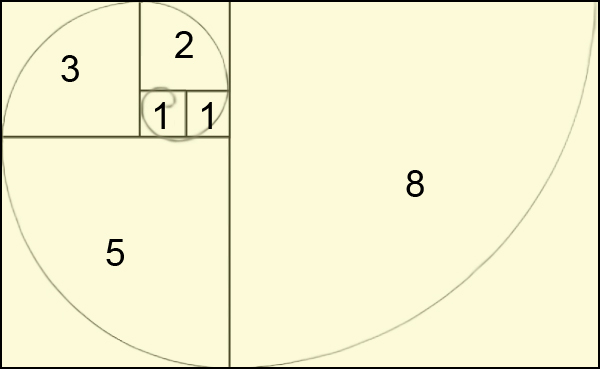
I could not talk about Fibonacci sequence without mention the golden ratio "phi". (phi=a/b=(a+b)/a=1.618033988...)
In the Fibonacci sequence, the ratio between two adjacent numbers(the bigger one divide the smaller one) are approching to the golden ratio phi by using the bigger numbers.
| A | B | C |
| 1 | 2 | 2 |
| 2 | 3 | 1.5 |
| 3 | 5 | 1.6666... |
| 5 | 8 | 1.6 |
| ... | ... | ... |
| 610 | 987 | 1.6180327... |
| 987 | 1597 | 1.6180344... |
| ... | ... | ... |
Golden ratio is used in many other areas besides mathematics, such as arts. As not only an artist but also a mathematician, Leonardo da Vinci had used the golden ratio in his art pieace, Mona Lisa. Only look at those rectangular box in this paiting, the size of those squares are exactly match with the Fibonacci sequence.
We can also find the Fibonacci numbers in nature, such as nautilus shell.
The Fibonacci sequence is also found be useful in stock trading. A professional and well-known accountant, Ralph Nelson Elliott discovered a principles and created stock analytical tools. This achievement has a strong connection with the Fibonacci sequence. Since I barely know the stock marketing, this link may help those of you who are interested in it: en.wikipedia.org/wiki/Elliott_Wave_Principle#Fibonacci_relationships
In the book/moviethe Da Vinci Code, the Fibonacci sequence plays a important role in the story clue. If you are interest in, you would have a lot of fun while reading/watching it!
Question/Comments:
- Are the images you posted copyrighted? If so, did you check that you are allowed to post them on a website? -Rhea team.
Answer:
- For the first image, mona lisa, it was found in the following link[1] and in this page it says this image is in the public domain in the U.S, so it is copyright-free.
- Good! -Rhea Team.
- I sincerely apology for the second image. I made a mistake while posting it. I thought it was also in public domain, but when I double checked again today then I realized it was not. I have already fixed it! These new images are both copyright-free. Sorry for the inconvenience. -Antong Li
- Thanks! -Rhea Team.