QE2007 CS-4 ECE580 - Rhea

1.(25 pts) State whether the following statements are true of false. No justification is necessary (a) (10 points) Let $ {N_{i}(t), t \geq 0, i=1,2,3,... K} $ be $ K $ independent Poisson Processes with rate $ \lambda $. Assume that $ K $ is a Poisson random variable independent of $ N_{i}(t) $ (for all i) and has mean a. Let $ N(t)=\sum_{i=1}^{K} N_{i}(t) $

i.(5 points) Statement: $ \{  N(t), t \geq 0 \} $ is a Poisson process with rate $ a \lambda $. 

ii. (5 points) Statement: For a given t and T, $  (N(t+T)-N(t))  $ is a Poisson random variable with mean $  a \lambda T  $. 

(b) (5 points) Statement: In the slow-start phase, TCP sender increases the congestion-window by 1 every round-trip time.
(c) (5 points) Consider a stationary packet-arrival process (i.e. assuming that it has started for infinite amount of time from the past). Let $ X_{i}, -\infty < i < \infty $ denote the inter-arrival time between the i-th packet and the (i+1)-th packet. Assume that for each i, $ X_{i} $ is i.i.d exponentially distributed. Let t denote an arbitrary time at which the packet stream is observed. Let S denote the amount of time between the time t and the arrival time of the last packet before t.
Statement: It then follows that

(d) (5 points) Statement: For a given utilization, the M/M/1 queue has the smallest average delay among all M/G/1 queueing systems.

Solution:
(a)
i. false ii. false
(b) false
(c) true
(d) false

2.(45 points) Consider the following single-server queueing system with an infinite buffer. Packets arrive according to a Poisson process with rate $ \lambda $. The size of each packet is i.i.d exponentially distributed with mean $ 1/ \mu $. The server has a capacity of 1. When there is only one packet in the system, the server will serve this packet at the rate of 1. Hence, a single packet with length $ l $ will take time $ l $ to complete service. However, whenever there are two or more packets in the system, the server sill split its capacity into two parts, and serve the first two packets in the queue simultaneously, each at the rate of 1/2. For example, if two packets arrive at an empty system at the same time, and both have size $ l $, then they will also complete service at the same time, after a time $ 2l $.
Let $ P_{m} $ denote the steady-state probability of having $ m $ packets in the queue.

(a) (15 points) Assume that at a particular time-instant $ t_{0} $, there are $ m $ packets in the queue, and $ m \geq 2 $. Let $ t_{0} + T $ denote the first time-instant after $ t_{0} $ when a packet completes service. Carefully derive the probability $ P[T \geq t] $ for all $ t $.
(b) (10 points) Draw the state transition diagram of the continuous time Markov chain that can be used to determine $ P_{m} $ .
(c) (10 points) Write down the balance equations for solving $ P_{m} $/
(d) (10 points) Compute $ P_{0} $, the probability that the system is empty.

Solution:
(a) Each packet needs time is an exponential distribution $ \frac{\mu}{m} e^{-\frac{\mu}{n} t} $
$ P(T \geq t) = (\int_{t}^{\infty} \frac{\mu}{m} e^{- \frac{\mu}{m}t} )^{m} $ $ = (e^{- \frac{\mu}{m}})^{m} = e^{-\mu t} $
(b)
(c) $ \lambda P_{m} = \mu P_{m+1} $
(d) $ P_{0}(1+ \rho + \rho^{2} + ...) = 1 $
$ P_{0} \cdot \frac{1}{1- \rho} = 1 $
$ P_{0} = 1 - \rho = 1 - \frac{\lambda}{\mu} $

3. (20 points)
Consider the network shown below. The labels on the links correspond to the probabilities of link failure. Assume that the links fail independently of each other. Let noda A be the source. Our goal is to find the most reliable path from the source A to every other node.

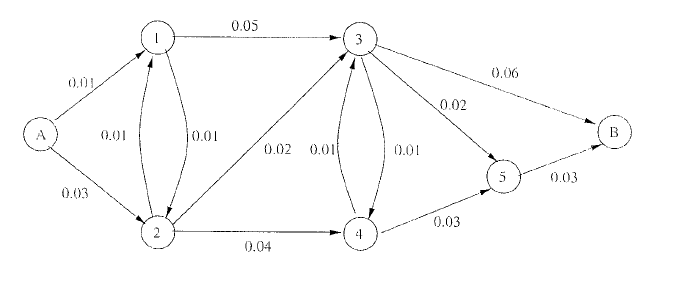
(a) (15 points) Provide a modified version of Dijkstra's algorithm to find the most reliable path from the source A to each node in the network above.
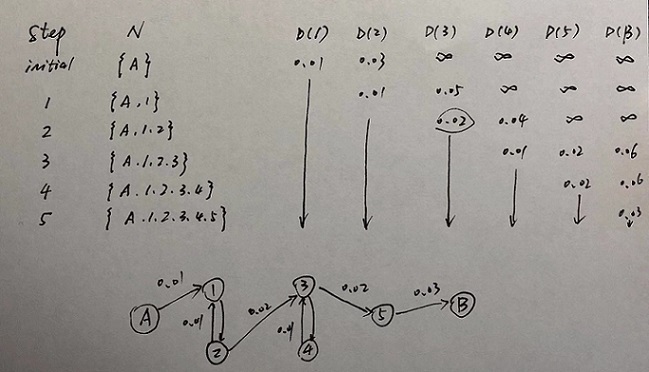
(b) (15 points) Apply your modified algorithm to the network above to find the most reliable paths from the source A to each node. Show at least three iterations.

Solution:

Back to ECE QE page