Contents
[hide]Practice Problem: Stationary Increment Property
Question
Explain what is the "stationary increment property" and why sum processes have this property.
You will receive feedback from your instructor and TA directly on this page. Other students are welcome to comment/discuss/point out mistakes/ask questions too!
Answer 1
The stationary increment property says that the difference between the values of a random process at two distinct times will result in a random variable with the same distribution as the random variable contained in the random process at the time found by differencing the two distinct times mentioned earlier.
Sum processes have this property because the difference between the values of a sum process at two distinct times yields a random variable defined by summing the values of an iid process from the earlier time until the later time. In addition, the random variable contained in the sum process at the time found by differencing the earlier and later times is found by summing the values of the same iid process from the initial time until the time found by differencing the earlier and later times. Because the process being summed in both cases is iid, the distributions of both random variables are the same and the sum process can be said to have the stationary increment property.
Answer 2
The stationary increment property can be explained intuitively by stating that the probability distribution of any increment is only a function of how long the increment is, and not where it is located on the time domain.
For example, if it had this property, $ X_{n} $ would have the same distribution as $ X_{2n}-X_{n} $ because the length of both of the increments is n.
Sum processes have this property because the random variables in the process are time-independent. The distribution of a random variable at t = 1 is the same as a random variable at t = 2. Therefore, the important variable is the length of time that the process is allowed to run, because this is what will change the sum. Changing the start time but keeping the length of time the same will not change the distribution.
Answer 3
A stochastic process X = {X_0, X_1, ..} has the stationary increment property (SIP) when, for all $ t > s > 0 $, the distribution of $ X_t - X_s = $ the distribution of $ X_{t-s} $. Eg if we let t = 5 and s = 2, the SIP would ensure that distribution of $ X_5 - X_2 = $ the distribution of $ X_3 $.
Now consider the i.i.d. (independent and indentically distributed) random process Z = {X_0, X_1, ..}. Eg, the consecutive rolling of a fair, six-sided die would be such and i.i.d. random process. Next, we define a discrete-time sum process S as:
$ S_n \triangleq \sum_{i=1}^{n} Z_i $
Therefore, our sum process S has the SIP iff:
$ joint pdf (\sum_{i=t-s+1}^{t} Z_i) = joint pdf(\sum_{i=1}^{t-s} Z_i) \;\;\; \forall t,s \; : \; t > s > 0. $
Eg for t = 5 and s = 2, we need to check: does the distribution of $ Z_5 + Z_4 + Z_3 = $ the distribution of $ Z_3 + Z_2 + Z_1 $?
We can conclude that for any $ X_t - X_s $ and $ X_{t-s} $, although these two sums are not generally independent (eg for the above example, a Z_3 term exists in both sums, therefore precluding independence), the two sums do possess identical distributions, therefore satisfying the SIP. This is because the distribution of *any* set of (t-s) distinct i.i.d. r.v.s is equivalent. Note that *any* in the previous statement makes a stronger claim than the SIP. That is, the (t-s) distinct i.i.d. r.v.s do not need to be consecutive, as we only care about the measure of i.i.d. r.v.s, and not their (distinct) indices. (In the DT case, 'measure' refers to the number of time steps.) Eg, the distribution of $ Z_5 + Z_3 + Z_1 = $ the distribution of $ Z_4 + Z_2 + Z_1 $. However, note that the distribution of $ Z_5 + Z_1 + Z_1 $ does not equal the distribution of $ Z_4 + Z_2 + Z_1 $, because the two $ Z_1 $s in the first sum are not distinct, and therefore are not independent.
Although the independent increment property (IIP) has not been covered above, here's a comparison:
SIP
. MEASURE of i.i.d. r.v.s must be equivalent . INDICES of the i.i.d. r.v.s may overlap, but must be distinct within a sum
IIP
. MEASURE of i.i.d. r.v.s does not matter . INDICES of the i.i.d. r.v.s must not overlap, but may be redundant within a sum
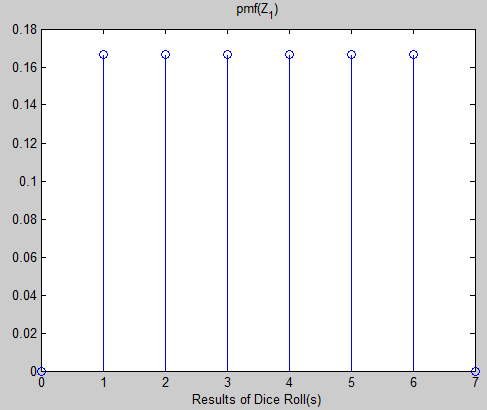
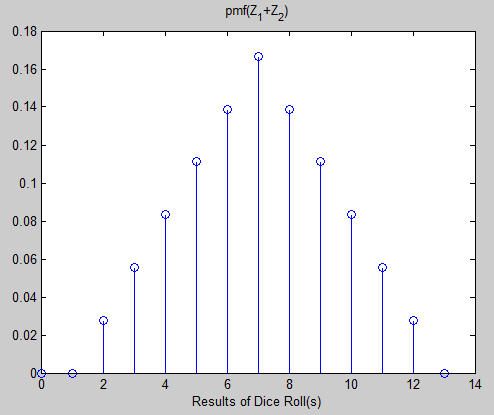
Finally, let's illustrate the SIP for a sum process composed of i.i.d. r.v.s Z that represent the outcome of the fair 6-sided dice roll previously mentioned. Below are the pmf and joint pmf that fully characterize the sum processes $ S_1 = Z_1 $ and $ S_2 = Z_1 + Z_2 $, respectively. For the SIP to hold w.r.t. the first pmf below, $ pmf(Z_1) $ must equal $ pmf(S_t - S_{t-1}) = pmf(Z_t) $. Likewise, for the SIP to hold w.r.t. the second pmf below, $ pmf(Z_1 + Z_2) $ must equal $ pmf(S_t - S_{t-2}) = pmf(Z_t + Z_{t-1}) $. Concerning the first pmf below, it's not hard to image that regardless of time, a single fair six-sided dice roll will have the same pmf as $ Z_1 $. Similarly, we can imagine that for any two dice rolls, regardless of where they occur in time (do not have to be consecutive), the pmf of the two dice rolls will be identical to $ pmf(Z_1 + Z_2) $. Though more tedious to compute the pmf of larger number of dice rolls, the SIP property will continue to hold.
Answer04
a)Stationary increments is for any s<t, Xt - Xs is equal in distribution to Xt-s. This means that the probability distribution of any increment Xs - Xt depends only on the length of time interval s-t; the increments on same time interval will result in the same probability distribution.
b)sum process is a stationary increments process because: Let a1, a2...be a sequence of iid variables. Then Xn = a1+a2 +...+an is a stationary increment process with respect to n, because the increment at time n is just an.
Answer 5
a) When a random process has the stationary increment property it means that for two different (non-overlapping) intervals [t0, t1] and [t2,t3] of the same length ([t3-t2] = [t1-t0]) in the time domain the pdf/pmf of these two intervals are the same.
b) Sum processes have the stationary increment property because their current value does not depend on any previous values. Their variables are iid (independent and identically distributed). An example is the random walk, each step does not depend on the last step the person took. With this in mind it does not matter when we start watching the person's footsteps, the probability function dictating his steps is the same.
Answer 6
a) The stationary increment property states that in a random process, any two non-overlapping, equally sized intervals have equal probability distribution functions. This could be summarized by saying that the probability distribution functions of a random process are only dependent on the size of the interval.
b) Sum processes must have this property because sum processes are time-independent and their specific results are independent of any previous result. This is because the sum process deals with independently and identically distributed variables, which means that the variables do not depend on each other and are also spaced out by a certain size throughout the process.
Answer 7
a.) The Stationary Increment Property of random processes is the property which claims that the probability distribution of that random process depends only on the time interval, not the absolute time at which the process occurs. For instance if I flip a coin as often as I can all day long, I'm equally likely to get a head in the first 5 minutes as I am in a 5 minute window an hour later (assuming I don't get tired).
b.) Sum processes have this property because they do not change over time. In a sum process I am counting events with a probability that is independent of the absolute time. For instance in the counting heads example, the coin retains a 50% chance of heads, and my flipping rate remains constant over time, therefore the number of heads in that interval only depends on how long I'm counting for!
----