Contents
[hide]Practice Problem: normalizing the probability mass function of a discrete random variable
A random variable X has the following probability mass function:
$ p_X (k) = \frac{C}{3^{|k|}}, \text{ for } k \in {\mathbb Z}, $
where C is a constant. Find the value of the constant C.
You will receive feedback from your instructor and TA directly on this page. Other students are welcome to comment/discuss/point out mistakes/ask questions too!
Answer 1
By axiom II (normalization), the following must hold:
$ \sum_{k \in \Omega} p_{X}^{k} = 1 $
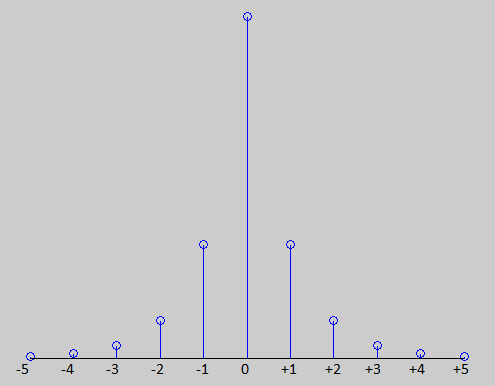
This implies that the (infinite) sum of probabilities must converge. Therefore, we're looking for the discrete summation of the following qualitative graph, which should = 1:
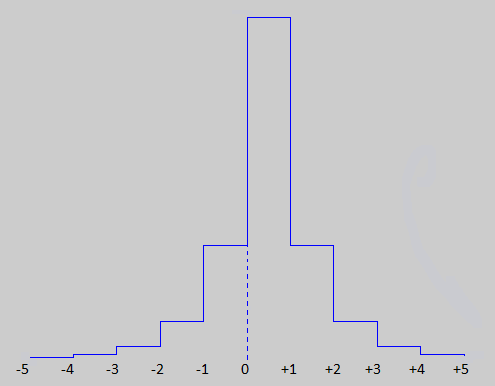
Or equivalently, the continuous integral of the following piecewise function, which should = 1 as well:
We can rearrange our initial sum into a geometric series:
$ \sum_{k \in \Omega} p_{X}^{k} = \sum_{k \in \Z} \frac{C}{3^{|k|}} = \sum_{k \in \Z^{-}} \frac{C}{3^{|k|}} + \frac{C}{3^{0}} + \sum_{k \in \Z^{+}} \frac{C}{3^{|k|}} $
$ = C + 2\sum_{k \in \N^{+}} \frac{C}{3^{k}} \;\;\; \because |-k| = |k| = k \;\;\; \forall \, k \in \Z $
$ = 2\sum_{k \in \N^{0}} \frac{C}{3^{k}} - C = 2C\sum_{k \in \N^{0}} (\frac{1}{3})^{k} - C $
It is now clear that we have a geometric series term of the following form:
$ \sum_{k=0}^{\infty} a^{k} = \frac{1}{1-a} \;\;\; \forall \, |a| < 1 $
Where our 'a' is (1/3). This yields:
$ 2C\frac{1}{1-\frac{1}{3}} - C = 2C\frac{3}{2} - C = 3C - C = 2C $
By our initial constraint of normalization:
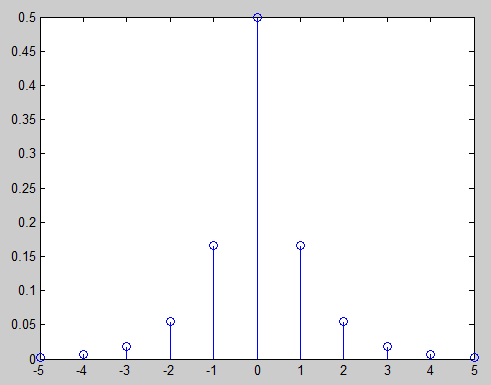
$ 2C = 1 \;\;\; \Rightarrow \;\;\; C = \frac{1}{2} $
Now we can label our qualitative graph with our solution:
Answer 2
Write it here.
Answer 3
Write it here.