One-Class Support Vector Machines for Anomaly Detection
In my research area (error detection in software systems), we typically want to perform 2-class classification. For example, we want to determine whether the condition of a system is normal (class 1) or abnormal (class 2) based on some metrics. However, sometimes we only have training data of one class, typically of normal behavior. In those cases, we cannot use traditional Support Vector Machines (SVM) because they are aimed for 2-class classification problems.
Support Vector Domain Description (SVDD) [1] is a technique that I have found useful for cases when we only have data of one class. It is essentially a modification of SVM to work in one-class scenarios. Here's a brief description of the technique summarized from [1].
Support Vector Domain Description
SVDD has been proposed in [1] for outlier or novelty detection. The basic idea is that it tries to find a hyper-sphere in the feature space which can enclose all (or almost all) the training data with the minimum volume. Mathematically, it is aimed to minimize the following objective $ F(R,a,\xi_i) = R^2 + C \sum_{i=1}^N \xi_i $ where $ a $ is the center of the sphere, $ R $ is the radius, $ C $ gives the trade-off between simplicity (or volume of the sphere) and the number of errors (number of target objects rejected), and $ \xi $'s are slack variables that have the same functionality as in traditional SVM for classification. This has to be minimized under the constraints: $ (x_i - a)^T (x_i - a) \leq R^2 + \xi_i\text{,} \qquad \xi_i \geq 0 $.
By incorporating those constraints into the objective function, we get the Lagrangian [1]:
$ L(R,a,\alpha_i,\xi_i) = R^2 + C \sum_{i=1}^N \xi_i - \sum_{i=1}^N \gamma_i \xi_i - \sum_{i=1}^N \alpha_i \left( R^2 + \xi_i - (x_i - c)^T (x_i - c) \right) $
with Lagrange multipliers $ \alpha_i, \gamma_i \geq 0 $. By setting the derivatives with respect to the primal variables $ c $, $ \xi_i $ and $ R $ to zero, we get $ c = \sum_{i=1}^N \alpha_i x_i $, $ 0\leq \alpha_i \leq C $, and $ \sum_{i=1}^N \alpha_i = 1 $.
Substituting the above formulas into the Lagrangian we obtain the following dual problem where we maximize with respect to $ \alpha_i $:
$ L = \sum_{i=1}^N \alpha_i (x_i^T \cdot x_i) - \sum_{i,j=1}^N \alpha_i \alpha_j (x_i^T \cdot x_i) $
with constraints $ \sum_{i=1}^N \alpha_i = 1 $ and $ 0 \leq \alpha_i \leq C $. Like in SVM, we can replace the inner product $ (x_i^T \cdot x_i) $ by any positive definite kernel $ K(x,x') $. Then, the resulting hyper-sphere will enclose data examples that are mapped into a high dimensional feature space. If we do so, we maximize with respect to $ \alpha_i $:
$ L = \sum_{i=1}^N \alpha_i K(x_i,x_i) - \sum_{i,j=1}^N \alpha_i \alpha_j K(x_i,x_j). $
To test whether a new data point $ x $ is within the spherical region (i.e. whether it is of normal behavior data or not), we evaluate the sign of
$ y(x) = \sum_{i=1}^N \alpha_i K(x,x_n) + b $
where the threshold parameter $ b $ is determined as in traditional SVM by summing $ \alpha_i K(x',x_i) $ for all the support vectors $ x' $, and then getting an average for the different values of $ b $. A new point $ x $ is said to be in the sphere if $ y(x) \geq 0 $, and outside the sphere if $ y(x) < 0 $. In terms of my research area, if a new point is in the sphere we say that the system is running normally, otherwise it is running abnormally.
Some Experiments
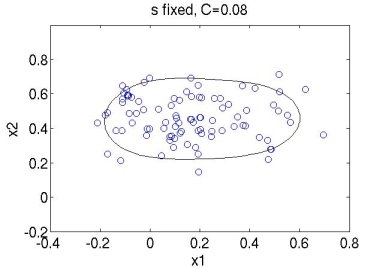
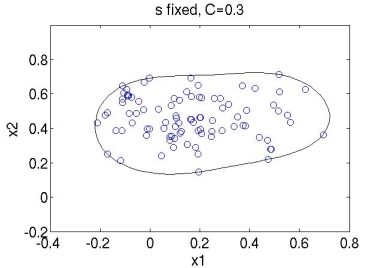
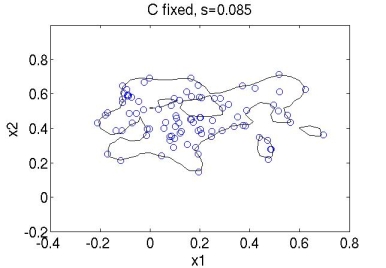
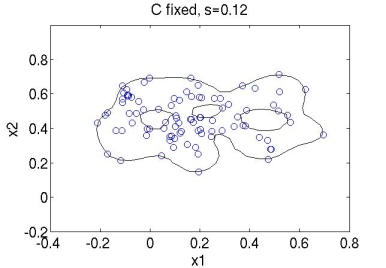
I have used the Gaussian kernel function $ K(x,x') = \text{exp}(-{\parallel x - x' \parallel}^2/{2 s^2}) $ to build the hyper-sphere using normal behavior data of a real system. When training SVDD we basically have to find the best values for parameters $ s $ and $ C $. Depending on these values the shape of the hyper-sphere and the amount of points that are allowed outside it will vary. Below are some plots for different values of these parameters (the code is all implemented in Matlab).
References
[1] D. M. J. Tax and R. P. W. Duin, "Support vector domain description," Pattern Recogn. Lett., 20(11-13):1191–1199, 1999.
--ilaguna 21:06, 20 April 2010 (EDT)