Work in Progress
Limits Approaching Infinity Intuitively
by Kevin LaMaster, proud Member of the Math Squad.
Contents
[hide]Introduction
I've noticed that many calculus one students loathe taking limits specifically as they approach infinity. This series should not be an introduction to limits nor should it replace a strict definition for a limit. Both of those can be found better at this tutorial. This only serves for a crash course tutor replacement for Calculus 1 students struggling with some difficult homework. If you wish you could solve limits like
$ \lim_{x\to\infty}sin(\frac{x^4-sqrt(2)x^2+e^{\pi}x}{x^{25}+x(x+2)(x-1)}) $
then stick around Or skip to the end. I'm a introduction not a cop
Basic Limits
Just as a recap over basic limits not into infinity.
Limits of Continuous functions
For the majority of limits the limit can just be found by plugging the values into the function.
Unfortunately the only limits most people are interested in are not these easy ones
For example $ \lim_{x\to 2}x^2+2x+1=2(2)^2+2(2)+1 $
The definition of a continuous function is that the limit at any point is equal to the value at that point.
The complicated math way to say this is $ \lim{x\to x_0}f(x)=f(x_0) $
This makes sense. If a function is continuous then every point is exactly where we would "expect it to be".
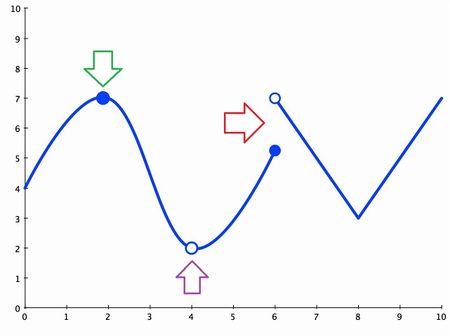
As you can see by the graph, the green arrow shows a point on the graph that is exactly where we would expect it to be. The graph is continuous at this point.
The purple arrow shows a place where we would expect a point, but there isn't one there. The graph isn't continuous at that point.
The red arrow shows a point where we don't know what to expect. Coming from the left it looks like the graph should be the lower point. But coming from the right we would expect it to be the higher point. Since the function can't do both it isn't continuous at this point. This topic of approaching a limit from one direction or another brings us to our next topic.
Directional Limits
In the case of the graph above we may want to know the limit as we approach a point strictly from the left or from the right. We show this in our limit with a small plus or minus sign floating above the value.
For example. $ \lim_{x\to 2^{-}}2x+1=5 $. Notice that just because its $ 2^{-} $ DOES NOT make it the same as $ -2 $. This means we take the limit as we approach the point 2 from numbers slightly less than 2. The same is true in reverse for $ 2^{+} $
Dividing by Zero and Infinity??
To set the record straight before we begin, infinity does not work like any other run of the mill number. It is, specifically by definition, not a number. A quick example of why not would be
$ \infty + 3=\infty\\ \infty - \infty + 3 =\infty - \infty\\ 3=0 $
As I'm sure you all have experienced, divide by zero errors are the bane of any mathematician. Lets try to find if there is a way to get close but not quite zero and see what that is. What better way to do this than with our new found tool. The limit.
Lets see what happens if we do $ \lim_{x\to 0}\frac{1}{x} $
We can't just plug it in like before and there's nothing we can cancel it out with, so lets just get closer and closer by hand.
If we try the following values:
| x | $ \frac{1}{x} $ |
|---|---|
| .1 | 10 |
| .001 | 1000 |
| .000001 | 1000000 |
This seems pretty pointless, the smaller the number we put in the bigger the number we get out seemingly without end. Let's just make a name for this concept of a value without an highest bound and call it fibigy or better yet infinity. (Note that we are not saying that infinity is this number but rather a concept for a value without anything higher than it)
Now that we've made this "new" term, $ \infty $, we can say that $ \lim_{x\to 0}\frac{1}{x}=\infty $
We can try a similar process in reverse with this new found term infinity
I wonder what $ \lim_{x\to\infty}\frac{1}{x} $ is?
What if we try the same method as before?
| x | $ \frac{1}{x} $ |
|---|---|
| 10 | .1 |
| 1000 | .001 |
| 1000000 | .000001 |
We know for sure that this value can never be negative since the numbers only get larger positive, and we know that the numbers will never stop getting lower.
Combined we can pick the smallest not negative number we can find, 0.
This makes sense $ \lim_{x\to\infty}\frac{1}{x}=0 $ and $ \lim_{x\to 0}\frac{1}{x}=\infty $
Now we can apply these two limits to problems that look much more difficult than they are.
CAUTION
- We cannot say that $ \frac{1}{0}=\infty $ for similar reasons to why we cannot use infinity as a number
- For example $ 1*\frac{1}{0}=\infty=\frac{2}{0}=2*\frac{1}{0} $
- $ 1=2 $
Application to harder looking problems=
But you didn't come here to read about boring basic limits, you came here cause there is some annoying limits that'll be on the calc exam and someone sent you to this tutorial. So lets get to work.
As I'm sure you know very few teachers will be so nice as to ask you what the $ \lim_{x\to\infity}\frac{1}{x} $ is on a test
They'll probably try to ask you something terrifying looking like
$ \lim_{x\to\infty}sin(\frac{x^4-sqrt(2)x^2+e^{\pi}x}{x^{25}+x(x+2)(x-1)}) $
As scary as that looks you have all the tools necessary to solve it.
Lets start with something a little bit easier
$ \lim_{x\to\infty}\frac{x}{x^2+1} $
If we just "plug in" infinity we get $ \frac{\infty}{\infty} $ and that can't be right
Please note just because it is $ \frac{\infty}{\infty} $ DOES NOT MEAN that it is 1
In the scheme of infinity what is another +1? $ \infty+1=\infty $ right?
So that means that when $ {x\to\infty},\frac{x}{x^2+1}=\frac{x}{x^2} $
Now we can reduce it a bit further by cancelling x's to $ \frac{1}{x} $
And we know that $ \lim_{x\to\infty}\frac{1}{x} $ from before!
Ok now lets step it up one more notch. What if we try $ \lim_{x\to\infty}\frac{x^3+1}{x^2+2x+1} $
Now we still have a pesky 2x term in there. But compared to $ \infty*\infty $ is $ \infty*2 $ really anything at all?
Lets reduce it then to $ \frac{x^3}{x^2}=x $ and we know that $ \lim_{x\to\infty}x=\infty $
Now lets try that really hard problem form the start.
$ \lim_{x\to\infty}sin(\frac{x^4-sqrt(2)x^2+e^{\pi}x}{x^{25}+x(x+2)(x-1)}) $
Lets just assume that the only terms that matter when it comes to infinity are the largest ones by far. That reduces this problem to
$ \lim_{x\to\infty}sin(\frac{x^4}{x^{25}}) $
Which we can cancel to get
$ \lim_{x\to\infty}sin(\frac{1}{x^{21}}) $
If $ \lim_{x\to\infty}\frac{1}{x}=0 $ then $ \lim_{x\to\infty}\frac{1}{x^{21}}=0 $ as well.
This means that $ \lim_{x\to\infty}sin(\frac{1}{x^{21}})=sin(0)=0 $
We just solved the hardest limit you'd thought you'd ever see.