Applications: Image Processing
In image processing, it is often necessary to find edges of shapes. Images are, by nature, complex maps of pixels, and thus can be very difficult for a computer to interpret and reduce into simple information. The Laplace operator is a tool used to solve some of these problems.
Consider, for example, a self-driving car. This vehicle must be able to interpret from an image what another object is, such as a car, stop sign, or pedestrian. Thus, edge detection is an important aspect of image processing. The Laplace operator is the perfect tool for this.
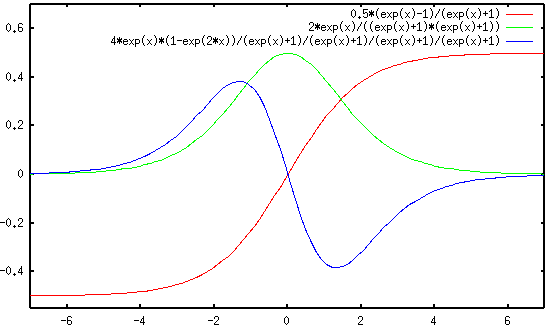
Take, for example, the above graph. Along the x-axis is a row or column of pixels. Along the y-axis is the relative brightness of the pixels. The red line graphs the relative brightness of the pixel over the position, the green line the first derivative, and the blue line the second derivative, which is analogous to the Laplace operator.
Where the red line is 0, the second derivative, analogous to the Laplace operator, is also zero. This indicates that there is an edge here, as it is the point at which the brightness of the pixel is changing the most.
What happens here is that the Laplace operator is used to calculate the Laplacian matrix of $ n $ pixels around the point in question. When the Laplace operator records values at 0, there is a 2-d "inflection point" where the brightness changes from increasing at an increasing rate to increasing at a decreasing rate (or vice-versa). This process is called the Laplace filter in image processing.
An example can be seen below:

The original image, before application of the Laplace filter.
The image with edge detection shown, after the use of the Laplace filter.
With its obvious connections to image processing, neural networks, and artificial intelligence, it is the opinion of the authors that the Laplace filter, and therefore the Laplace operator, will continue to be used extensively.
Examples of code can be found at "OpenCV Laplace Filter Image Processing" in the Links for Further Reading section.


