Applications: Harmonic Functions
Definition
Harmonic functions are functions that satisfy the equation
$ \frac{\partial^{2} f}{\partial x_{1}^{2}}+\frac{\partial^{2} f}{\partial x_{2}^{2}}+\cdots+\frac{\partial^{2} f}{\partial x_{n}^{2}}=0 $, or $ \large\Delta f = \nabla^{2} f = 0 $.
A concurrent definition for a harmonic function is the idea that the value at a point in a function is always equal to the average of the values along a circle surrounding that point. This leads to an interesting conclusion about the Laplace Operator itself, in that when $ \Delta f = 0 $, the above statement is true.
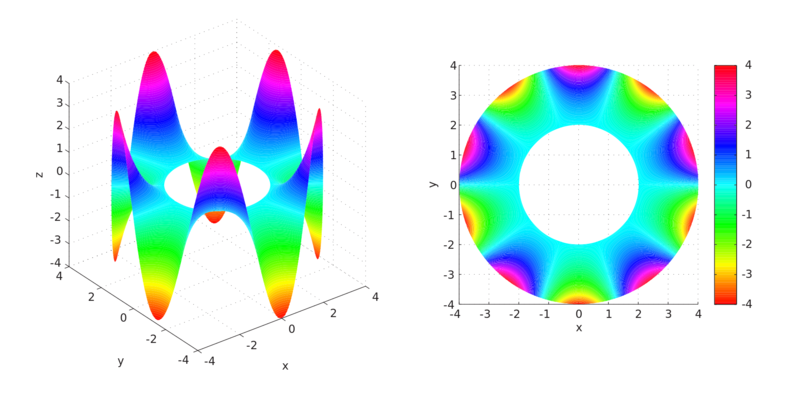
Harmonic Function in x, y, and z defined on the area between a circle of radius two and a circle of radius four.
Harmonic functions are extremely useful functions, as they are potential functions. This means that they are similar to the conservative functions studied this year on the topic of divergence. Harmonic functions are useful in various branches of physics, as they can be used to reduce complex, three-dimensional functions into simpler, one dimensional functions. This is similar to how potential functions can be used to simplify the solutions of a divergence problem. Thus, since potential functions are harmonic functions, and vice-versa, every time we wrote a potential function we were actually writing a harmonic function, on that satisfies the above criteria and can be written in the form $ \Delta f = 0 $.