Homework 9 Solutions, ECE301 Spring 2011 Prof. Boutin

Students should feel free to make comments/corrections or ask questions directly on this page.

Question 1

(a) The given signal has finite duration and hence it is not band-limited.

(b) The given signal has finite duration and hence it is not band-limited.

(c) The given signal has infinite duration and hence it is band-limited.

$ x(t)=\frac{\sin(3\pi t)}{t}=\pi\frac{\sin(3\pi t)}{\pi t} $

$ \begin{align} \mathcal{X}(\omega)&=\pi \cdot \mathfrak{F}\left\{\frac{\sin(3\pi t)}{\pi t}\right\} \\ &=\left\{\begin{array}{ll} \pi , & \mbox{ for } |\omega|<3\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \end{align} $

Thus the Nyquist rate of this signal is ω_s = 2(3π) = 6π.

QUESTION: I know that the answer to this isn't necessary to answer the question, but if the transform pair says that
$ \frac{2 \sin \left( W t \right)}{\pi t } \ $ transforms to $ \left\{\begin{array}{ll}1, & \text{ if }|\omega| <W,\\ 0, & \text{else.}\end{array} \right. \ $,

then why does the F.Transform not account for the factor of "2" in front in the answers above and below?

Should the answers not take the following form:
$ \begin{align} \mathcal{X}(\omega)&=\pi/2 \cdot \mathfrak{F}\left\{\frac{2\sin(3\pi t)}{\pi t}\right\} \\ &=\left\{\begin{array}{ll} \pi/2 , & \mbox{ for } |\omega|<3\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \end{align} $
?

There was a typo in the CTFT pairs posted. There is no inherent '2' in the equation for the pair. To reference, the book will confirm this in the tables around page 329.

(d) The given signal has infinite duration and hence it is band-limited.

Instructor's note: it is not always the case that infinite duration signals are band-limited. However, it is true that finite duration signals are never band-limited. -pm

$ x(t)=\frac{\sin(3\pi(t+5))}{t+5}=\pi\frac{\sin(3\pi(t+5))}{\pi(t+5)} $

$ \begin{align} \mathcal{X}(\omega)&=\pi \cdot \mathfrak{F}\left\{\frac{\sin(3\pi (t+5))}{\pi (t+5)}\right\} \\ &=\left\{\begin{array}{ll} \pi e^{5j\omega} , & \mbox{ for } |\omega|<3\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \end{align} $

Thus the Nyquist rate of this signal is ω_s = 2(3π) = 6π.

Question 2

$ x(t)=e^{j\pi t}\frac{\sin(\pi t)}{t}=\pi e^{j\pi t}\frac{\sin(\pi t)}{\pi t} $

Using frequency shift property of FT, we get:

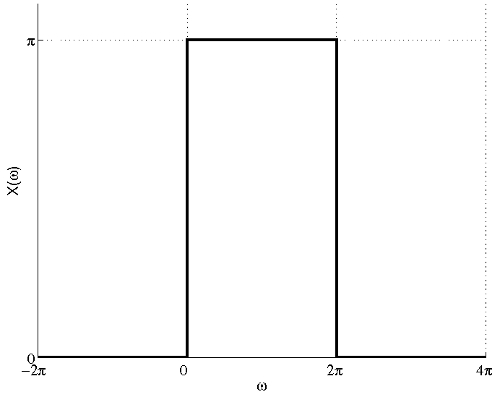
$ \begin{align} \mathcal{X}(\omega)&=\left\{\begin{array}{ll} \pi , & \mbox{ for } |\omega - \pi|<\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \\ &=\left\{\begin{array}{ll} \pi , & \mbox{ for } -\pi <\omega-\pi<\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \\ &=\left\{\begin{array}{ll} \pi , & \mbox{ for } 0<\omega<2\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. \end{align} $

The figure below shows the plot of the FT of x(t).

After sampling with a sampling period T, we get:

$ \mathcal{X}_s(\omega)=\frac{1}{2\pi}\mathcal{X}(\omega)*\mathcal{P}(\omega)=\frac{1}{T}\sum_{k=-\infty}^{\infty}\mathcal{X}(\omega-\frac{2\pi k}{T}) $

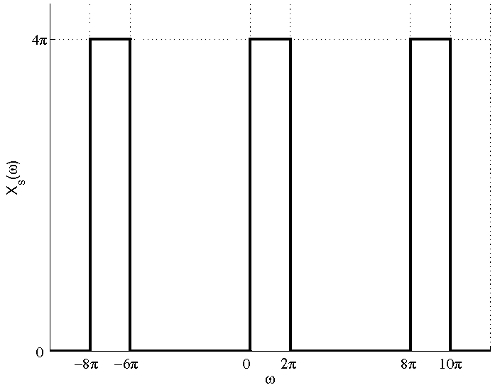
(a) The FT of the signal after sampling with sampling period $ T=\frac{1}{4} $ is shown in the figure below.

Instructor's note: Note that this is the Fourier transform of the CT signal representing the sampling in CT. The Fourier transform of the DT signal obtained by storing the values of the samples in an array, x_d[n] = x(n'T) is a frequency-rescaled version of this graph (in such a way to obtain a signal that is periodic with period 2π). -pm

From the figure, we can see that there is no aliasing and the signal can be recovered by filtering the sampled signal using the following filter:

$ \mathcal{H}(\omega)=\left\{\begin{array}{ll} \frac{1}{4} , & \mbox{ for } 0<\omega<2\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. $

Instructor's note: To recover the signal from the sampling in DT, one must first convert the samples to a pulse-train, and then low-pass filter. -pm

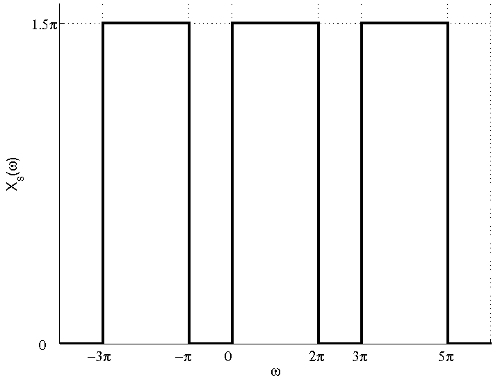
(b) The FT of the signal after sampling with sampling period $ T=\frac{2}{3} $ is shown in the figure below.

From the figure, we can see that there is no aliasing and the signal can be recovered by filtering the sampled signal using the following filter:

$ \mathcal{H}(\omega)=\left\{\begin{array}{ll} \frac{2}{3} , & \mbox{ for } 0<\omega<2\pi \\ 0, & \mbox{ elsewhere} \end{array}\right. $

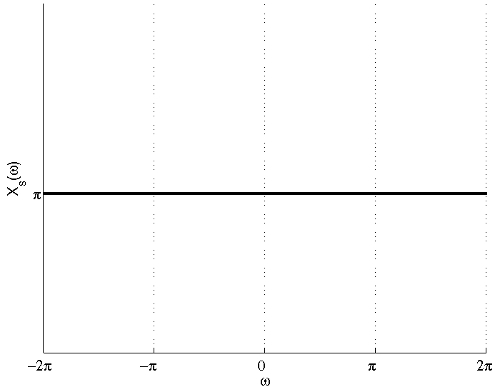
(c) The FT of the signal after sampling with sampling period T = 2 is shown in the figure below.

From the figure, we can see that there is aliasing and thus the signal cannot be recovered.

Question 3

$ \begin{align} \mathfrak{F}\left\{p(t-3)\right\}&=P(\omega)e^{-3j\omega} \\ &=\omega_se^{-3j\omega}\sum_{k=-\infty}^{\infty} \delta(\omega-\omega_s k) \\ &=\omega_s \sum_{k=-\infty}^{\infty} e^{-3j\omega_s k}\delta(\omega-\omega_s k) \text{ Using sampling property of dirac-delta function} \end{align} $

Let x_s(t) = x(t)p(t − 3), then

$ \begin{align} \mathcal{X}_s(\omega)&=\frac{\omega_s}{2\pi} \mathcal{X}(\omega)*\sum_{k=-\infty}^{\infty}e^{-3j\omega_s k}\delta(\omega-\omega_s k) \\ &=\frac{\omega_s}{2\pi} \sum_{k=-\infty}^{\infty}e^{-3j\omega_s k}\mathcal{X}(\omega-\omega_s k) \\ \end{align} $

Note that the exponential term does not depend on ω, and that at k = 0 it is 1. Thus:

if ω_s > 2ω_M, then the signal can be recovered by passing x_s(t) through the following filter:

$ \mathcal{H}(\omega)=\left\{\begin{array}{ll} \frac{2\pi}{\omega_s} , & \mbox{ for } |\omega|<\omega_M \\ 0, & \mbox{ elsewhere} \end{array}\right. $

if ω_s < 2ω_M, then there will be aliasing and the signal cannot be recovered.

What is ωm in this filter? I thought the cutoff for the filter needed to be ωc, where ωm < ωc < ωs - ωm, in order to remove all of the copies but retain the main signal.

--Kellsper 19:44, 21 April 2011 (UTC)

TA's comment: Yes, that is true. In this case $ \omega_c=\omega_M $.

Question 4

Since x(t) is sampled with a sampling period T_s = π / ω₀, then the sampling rate is ω_s = 2ω₀ and hence there is no aliasing.

Taking the FT of both sides of the system equation we get:

$ \mathcal{Y}(\omega)=j\omega\mathcal{X}(\omega) $

and hence the frequency response of the CT system is:

$ \mathcal{H}(\omega)=j\omega $

Using the relationship between the frequency response of the CT system and the DT system, we get:

$ \begin{align} \mathcal{H}_d(\omega)&=\mathcal{H}(\frac{\omega}{T_s}) \text{ for }|\omega|<\pi \\ &=j\frac{\omega}{T_s} \text{ for }|\omega|<\pi \end{align} $

Now in order to get the impulse response of the DT system we take the IDTFT of the frequency response above:

$ \begin{align} h_d[n]&=\frac{1}{2\pi}\int_{-\pi}^{\pi}j\frac{\omega}{T_s} e^{j\omega n} d\omega\\ &=\frac{j}{2\pi T_s} \int_{-\pi}^{\pi} \omega e^{j\omega n}d\omega \\ &=\frac{j}{2\pi T_s} \left[\omega \frac{e^{j\omega n}}{jn}\right]^{\pi}_{-\pi} + \frac{j}{2\pi T_s}\left[\frac{e^{j\omega n}}{n^2}\right]_{-\pi}^{\pi} \\ &=\frac{1}{2T_s n} [e^{j \pi n}+e^{-j \pi n} ] + \frac{j}{2\pi T_s n^2}[e^{j \pi n} - e^{-j \pi n}] \\ &=\frac{(-1)^n}{T_s n} \\ &=\frac{\omega_0 (-1)^n}{\pi n} \end{align} $

Note that an impulse response is sufficient to characterize an LTI system.

HW9

Back to 2011 Spring ECE 301 Boutin