Contents
[hide]Practice Question on Computing the Fourier Series continuous-time signal
Obtain the Fourier series the CT signal
$ x(t) = \left\{ \begin{array}{ll} 1, & \text{ for } -5\leq t \leq 5,\\ 0, & \text{ for } 5< |t| \leq 10, \end{array} \right. \ $
x(t) periodic with period 20.
You will receive feedback from your instructor and TA directly on this page. Other students are welcome to comment/discuss/point out mistakes/ask questions too!
Answer 1
$ k=0\, $
$ a_0=\frac{1}{20}\int_{-10}^{10}x(t)e^{-0}dt=\frac{1}{20}\int_{-5}^{5}1dt=\frac{1}{2} $
$ k\ne0 $
$ a_k=\frac{1}{20}\int_{-10}^{10}x(t)e^{-jkw_0t}dt=\frac{1}{20}\int_{-5}^{5}e^{-jk\frac{\pi}{10}t}dt=\frac{1}{20}\Bigg[\frac{e^{-jk\frac{\pi}{2}}-e^{jk\frac{\pi}{2}}}{-jk\frac{\pi}{10}}\Bigg]=\frac{1}{-jk2\pi}\Bigg(e^{-jk\frac{\pi}{2}}-e^{jk\frac{\pi}{2}}\Bigg) $
$ x(t)=\frac{1}{2}e^{-jk\frac{\pi}{10}t}+\sum_{k=-\infty}^-1\frac{1}{-jk2\pi}\Bigg(e^{-jk\frac{\pi}{2}}-e^{jk\frac{\pi}{2}}\Bigg)e^{-jk\frac{\pi}{10}t}+\sum_{k=1}^\infty\frac{1}{-jk2\pi}\Bigg(e^{-jk\frac{\pi}{2}}-e^{jk\frac{\pi}{2}}\Bigg)e^{-jk\frac{\pi}{10}t} $
--Cmcmican 21:35, 7 February 2011 (UTC)
- TA's comment: That looks fine. The expression for $ a_k $ is better written in terms of a sin function, though. Regarding the synthesis of $ x(t) $, you got it wrong actually. The complex exponentials should not have a minus sign in their exponents and for $ k=0 $ the complex exponential has a frequency of zero (DC).
- Another thing is that you may also further simplify $ x(t) $ and write it in terms of sin waves only. You will actually notice some pattern in the frequencies of these sin waves.
Answer 2
First I plotted it out, thanks to WolframAlpha 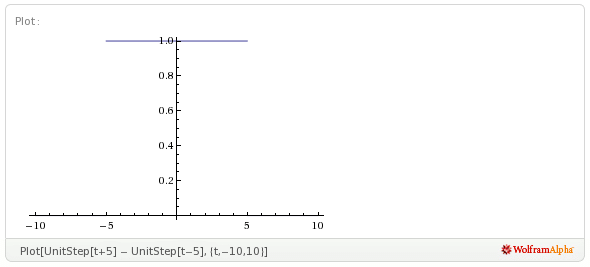
Then I used the equation $ a_{k} = \frac{1}{T}\int_{0}^{20}x(t)e^{-jk(\frac{2\pi}{T})t}dt $ where T = 20. You can change the limits of the integral to -10 and 10 since the function is periodic. We just need it over one period.
Solving for $ a_{0} $ first we get $ a_{0} = \frac{1}{20} \int_{-10}^{10}x(t)e^{-j(0)(\frac{2\pi}{20})t}dt $. We know that x(t) = 0 except for -5 < t < 5 where it is 1.
$ a_{0} = \frac{1}{20} \int_{-5}^{5}(1)e^{(0)}dt = \frac{1}{20}x \bigg|_{-5}^{5} = \frac{1}{2} $
$ a_{k} = \frac{1}{20}\int_{-5}^{5}(1)e^{-jk(\frac{2\pi}{20})t}dt; \text{ where } -5 < k <5 \text{ and }k \neq 0 $
$ a_{k} = \frac{1}{20} \left[ \frac{e^{-jk(\frac{\pi}{10})t}}{-jk(\frac{\pi}{10})}\right]_{-5}^{5} $
$ a_{k} = \frac{1}{20}\left(\frac{1}{-jk\frac{\pi}{10}}\right) \left[ e^{-jk(\frac{\pi}{10})5} - e^{-jk(\frac{\pi}{10})(-5)} \right] $
$ a_{k}= \frac{-1}{2jk}\left[ e^{-\frac{jk\pi}{2}} - e^{\frac{jk\pi}{2}} \right]\text{ for }-5 < k < 5\text{ and }k \neq 0\text{, all others }0 $
$ x(t) = \sum_{k=-\infty}^{\infty}a_{k}e^{jk\frac{2\pi}{T}t} $
$ x(t) = \sum_{k=-5}^{-5} a_{k}e^{jk\frac{ \pi}{10}t} $ I changed the limits of the sum because $ a_{k} $ is 0 for anything outside that range.
Answer 3
Write it here.

