1) a) $ \Gamma = \frac{Z_{in} - Z_1}{Z_{in} + Z_1} $
$ k_1 = \omega\sqrt{\mu_1\epsilon_1}\to n_1=\sqrt{\frac{\mu_1}{\epsilon_1}}\hspace{0.5cm}\nabla\times\bar{H}=\sigma\bar{E}+j\omega\epsilon E $
$ k_2 = \omega\sqrt{\mu_2\epsilon_2}\to n_2=\sqrt{\frac{\mu_2}{\epsilon_2}}\hspace{1.0cm}=\bigg(\epsilon+\frac{\sigma}{j\omega}\bigg)\bar{E} $
$ Z_{in} = Z_2 \bigg[\frac{Z_L+jZ_2\tan(\beta_2d)}{Z_2+jZ_L\tan(\beta_2d)}\bigg] $ $ Z_2 = n_2\:\:\:\:\: Z_L = n_c=\sqrt{\frac{\mu}{\epsilon_c}} = 0 (PEC) \begin{cases}\epsilon_c =\bigg(\epsilon+\frac{\sigma}{j\omega}\bigg)\\\sigma\to\infty\to\epsilon_c\to\infty\\\text{ then }M_c=0 \end{cases} $
$ Z_{in}=n_2\bigg[\frac{jn_2\tan(\beta_2d)}{n_2}\bigg] = jn_2\tan(\beta_2d) $
$ Z_1 = n_1 $
$ \Gamma = \frac{jn_2\tan(\beta_2d) -n_1}{jn_2\tan(\beta_2d) +n_1}\:\:\:\:\:(\beta_2 = k_2) $
$ \bar{E} = \bar{E}_i+\bar{E}_r = \hat{x}E_ie^{-jk_1z} + \hat{x}\Gamma E_ie^{+jk_1z} $
$ \bar{E} = \hat{x}E_i e^{-jk_1z} + \hat{x}E_i\Bigg[\frac{j\sqrt{\frac{\mu_2}{\epsilon_2}}\tan(k_2d) - \sqrt{\frac{\mu_1}{\epsilon_1}}}{ j\sqrt{\frac{\mu_2}{\epsilon_2}}\tan(k_2d) + \sqrt{\frac{\mu_1}{\epsilon_1}}}\Bigg]e^{+jk_1z} $
------------------------------------------------------------------------------------
b-i)$ \tan\big(\frac{\pi}{2}\big) = \infty $
$ \bar{E} = \hat{x}E_i \bigg[1+\frac{j}{j}\bigg] = \hat{x}(2E_i) $
------------------------------------------------------------------------------------
b-ii)
$ \tan(\pi) = 0 $
$ \bar{E} = \hat{x}E_i [1-1] = 0 $
------------------------------------------------------------------------------------ 2) $ \nabla\times\bar{E} = -\frac{d}{dt}B $ $ \oint\bar{E}\cdot dl = - \frac{d}{dt}\int_S\bar{B}\cdot ds = V_{EMF} $ --- if b>>a, there is no net flux through the outer loop, so, $ \oint \bar{E}\cdot d\bar{l}= 0 $ $ V_induced = 0 $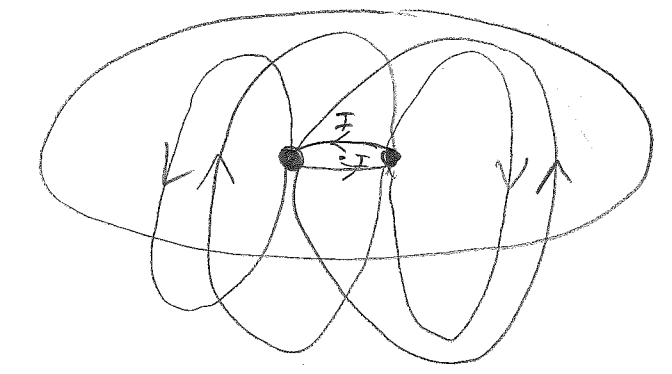
components cancel
------------------------------------------------------------------------------------ 3) $ \nabla\times\bar{H} = \bar{J}+\frac{\partial D}{\partial t}\hspace{1cm}dl = dr\hat{r}+r d\phi\hat{\phi} + dz \hat{z} $ $ \nabla\times\bar{E} = - \frac{\partial B}{\partial t} $ $ \oint\bar{E}\cdot dl = -\frac{\partial}{\partial t}\int_S\bar{B}\cdot ds = +\frac{\partial B}{\partial t}(\pi a^2) \hspace{0.5cm}\frac{\partial b}{\partial t}(-\hat{z}) $
$ \int_0^{2\pi}E_{\phi}r d\phi = +\frac{\partial B}{\partial t}(\pi r^2) $
$ \bar{E} = +\frac{\partial B}{\partial t}\bigg(\frac{\pi r^2}{2\pi r}\bigg)\hat{\phi} $
$ \bar{E} = +\frac{\partial B}{\partial t}\bigg(\frac{r}{2}\bigg)\hat{\phi} $
$ \bar{J}_\phi = \sigma \bar{E} $
$ I = \oint_S \bar{J}_\phi\cdot ds_\phi $
$ =\int_0^l\int_0^a\sigma E(dr dz) $
$ =\int_0^l\int_0^a +\frac{\partial B}{\partial t}\bigg(\frac{\sigma r}{2}\bigg)dr dz $
$ I = +\frac{\partial B}{\partial t}\bigg(\frac{\sigma a^2l}{4}\bigg) $
$ \mu = IA\hat{n} = +\bigg(\frac{\sigma a^2 l}{4}\bigg)(\pi a^2)\hat{z} $
$ \mu = +\frac{\partial B}{\partial t}\bigg(\frac{\pi\sigma l a^4}{4}\bigg)\hat{z} $
$ \tau = \mu\times B_0\hat{x} $
$ \tau = +\frac{\partial B}{\partial t}\bigg(\frac{\pi\sigma l a^4}{4}\bigg)B_0(\hat{y}) $ into page