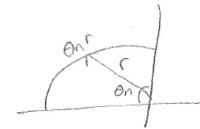
A)
$ \begin{align*} \bar{E} = \bar{E}_{10}&\exp[-j\beta_1(-x\sin\theta_1 + z\cos\theta_1) + j\omega_1t]\\ &+\bar{E}_{20}exp[-j\beta_2(-x\sin\theta_2 + z\cos\theta_2) + j\omega_2t] \text{ at z=0}\\ \bar{E} = \bar{E}_{10}&\exp[j\beta_1\times\sin\theta_1 + + j\omega_1t]+\bar{E}_{20}exp[j\beta_2\times\sin\theta_2 + j\omega_2t]\\ \end{align*} $
$ \begin{align*} P &= \frac{1}{2} Re[E\times H^*] = \frac{1}{2n_0}|\bar{E}|^2 \text{ assume: } \beta_1 = \beta_2 \\ &= \frac{1}{2n_0}\big[E_{10}^2 + E_{20}^2 + 2E_{10}E_{20}\cos[\beta\times(\sin\theta_1-\sin\theta_2) +(\omega_1-\omega_2)t]\big] \end{align*} $
$ \omega_1 = \omega_2 \to P = \frac{1}{2n_0}\big[E_{10}^2 + E_{20}^2 + 2E_{10}E_{20}\cos[\frac{2\pi x}{\lambda}(\sin\theta_1-\sin\theta_2)\big] \\ $
wave along
$ x = \cos\big(\frac{2\pi x}{\Omega}\big)\\ $
$ \Omega = \frac{\lambda}{|\sin\theta_1 - \sin\theta_2|} = \frac{1.0\cdot10^{-6}}{2\sin(0.01)}\approx \frac{10^{-6}}{0.02} = 5\cdot 10^{-5}m\\ $
B)
$ \begin{align*} \text{phase} = \big(\frac{2\pi}{\lambda}\big)\times(\sin\theta_1-\sin\theta_2) +(\omega_1-\omega_2)t &=\text{ constant}\\ \big(\frac{2\pi}{\lambda}\big)\big(\frac{dx}{dt}\big)(-\sin\theta_2-\sin\theta_2) + \triangle \omega &= 0, \beta =\frac{2\pi}{\lambda}\\ \frac{dx}{dt} = v_p = \frac{\triangle\omega}{2\beta\sin\theta_2} \cong \frac{2\pi\cdot10^7}{4\pi(10^6)(0.01)} &= 500m/s \end{align*} $
C)
$ \begin{align*} \bar{E} &= (E_{10}\hat{z})e^{-j(\beta_1x-\omega_1t)}+(E_{20}\hat{z})e^{-j(\beta_2x-\omega_2t)}\\ P&=\frac{1}{2n_0}\big[E_{10}^2 + E_{20}^2 + 2E_{10}E_{20}\cos[(\omega_1-\omega_2)t - (\beta_1-\beta_2)x]\big]\\ \text{phase }&= (\omega_1-\omega_2)t - (\beta_1-\beta_2)x = \text{ constant}\\ \frac{dx}{dt} &= v_p =\frac{\triangle\omega}{(\beta_1-\beta_2)}\\ \beta &= \omega\sqrt{\mu_0\epsilon_0}\sqrt{\epsilon_r} =\beta_0\sqrt{\epsilon_r} = \frac{2\pi}{\lambda_0}\sqrt{\epsilon_r(\omega)}\\ \frac{dx}{dt} &= \frac{\triangle\omega}{\frac{2\pi}{\lambda_0}(\sqrt{\epsilon_r(\omega_1)}-\sqrt{\epsilon_r(\omega_2)})}\\ \frac{dx}{dt} &= \frac{\triangle\omega}{\frac{2\pi}{\lambda_0}(\sqrt{\epsilon_r(\omega_0)+\epsilon_r(\omega_0)(\omega_1-\omega_0)}-\sqrt{\epsilon_r(\omega_0)+\epsilon_r(\omega_0)(\omega_2-\omega_0)})}\\ \end{align*} $
D)
$ \begin{align*} E = \sum_{n=-N/2}^{n=N/2}&E_0 \exp[-j\beta(-x\sin(n\triangle\theta)-\omega_0t)]\\ &\approx \sum_{n=-N/2}^{N/2}E_0 \exp[j\beta(xn\triangle\theta)+\omega_0t)] \end{align*} $ \end{enumerate}
a)
$ \bar{E}_i = \bar{E}_{10}e^{-j(2\pi/\lambda_1)(-\sin\theta_1x+\cos\theta_1z)}e^{j\omega_1t} + \bar{E}_{20}e^{-j(2\pi/\lambda_2)(-\sin\theta_2x+\cos\theta_2z)}e^{j\omega_2t} $
b)
$ \begin{align*} \omega_1 &= \omega_2 \to \beta_1 = \beta_2 = \frac{2\pi}{\lambda} = \omega\sqrt{\mu\epsilon}\\ \bar{E}_i|_{z=0} &= \bar{E}_{10}e^{-j(\frac{2\pi}{\lambda})(-\sin\theta_1x)}e^{j\omega_1t}+\bar{E}_{20}e^{-j(\frac{2\pi}{\lambda})(-\sin\theta_2x)}e^{j\omega_2t}\\ P_{ave} &= \frac{1}{2}Re(\bar{E}\times\bar{H}^*) = \frac{1}{2n_0}|E||E^*| \end{align*} $
$ \begin{align*} P_{ave} = \frac{1}{2n_0}[E_{10}^2 &+ E_{20}^2 + E_{10}E_{20}e^{-j(\frac{2\pi}{\lambda})[-\sin\theta_1x +\sin\theta_2x]}e^{j(\omega_1-\omega_2)t}\\ &+ E_{20}E_{10}e^{+j(\frac{2\pi}{\lambda})[-\sin\theta_1x +\sin\theta_2x]}e^{j(\omega_2-\omega_1)t}] \end{align*} $
$ \begin{align*} P_{ave} = \frac{1}{2n_0}\bigg\{E_{10}^2 + E_{20}^2 + 2E_{10}E_{20}\cos\bigg[\frac{2\pi}{\lambda}(-\sin\theta_2x -\sin\theta_1x)+(\omega_2-\omega_1)t\bigg]\bigg\} =0\\ \end{align*} $
constant phase also $ \omega_1=\omega_2 $ here.
$ \cos\big(\frac{2\pi x}{\Omega}\big)\\ \Omega = \frac{\lambda}{\sin\theta_2-\sin\theta_1} $
c)
$ P_{ave} = \frac{1}{2n_0}\bigg\{E_{10}^2 + E_{20}^2 +2 E_{10}E_{20}\cos\bigg[\frac{2\pi}{\lambda}x(\sin\theta_2 -\sin\theta_1)+(\omega_2-\omega_1)t\bigg]\bigg\} \\ $
$ \begin{align*} v = \frac{(\omega_2-\omega_1)\Omega}{2\pi}\\ \frac{x2\pi}{\Omega} +(\omega_1-\omega_2)t &= \text{ constant} \\ \frac{dx}{dt}\big(\frac{2\pi}{\Omega}\big) +(\omega_1-\omega_2)&=0\\ \frac{dx}{dt} = \frac{(\omega_1-\omega_2)\Omega}{2\pi} \end{align*} $
d)
$ \beta = \omega\sqrt{\mu_0\epsilon_0} = \frac{2\pi}{\lambda}\hspace{2cm} \omega_0=\frac{\omega_1+\omega_2}{2}\\ \beta_{new} = \omega\sqrt{\mu_0\epsilon_0}\sqrt{\epsilon_r} = \frac{2\pi}{\lambda} = \beta\sqrt{\epsilon_r} = \frac{2\pi\sqrt{\epsilon_r}}{\lambda}\\ \lambda = \frac{\lambda}{\sqrt{\epsilon_r(\omega)}} $
$ \begin{align*} P_{ave} &= \frac{1}{2n_0}\bigg\{E_{10}^2 + E_{20}^2 +2 E_{10}E_{20}\cos\bigg(\frac{2\pi}{\lambda}z(\cos\theta_1 +\cos\theta_2)+(\omega_2-\omega_1)t\bigg)\bigg\} \\ &=0 \end{align*} $
$ z\bigg(\frac{2\pi}{\lambda}\bigg)(\cos\theta_1+\cos\theta_2) + (\omega_2-\omega_1)t = \text{ constant} \frac{dz}{dt} = \frac{(\omega_1-\omega_2)\lambda}{2\pi(\cos\theta_1+\cos\theta_2)} \frac{dz}{dt} = \frac{(\omega_1-\omega_2)\lambda}{2\pi\sqrt{\epsilon_r(\omega_0) + \epsilon_r(\omega_0)(\omega-\omega_0)}} \hspace{1cm} \lambda = 2\pi c $
e)
$ \bar{E}_i = \sum_{n=-N/2}^{N/2}\bar{E}_0e^{-j[(2\pi/\lambda)(-\sin\theta_nx+\cancelto{0}{\cos\theta_nz})-\omega_0t]}\hat{y} = \sum_{n=-N/2}^{N/2}\bar{E}_0e^{-j(\theta_0 + \delta_n)}\\ \to \theta_0+\delta_n = \big(\frac{2\pi}{\lambda}\big)(x)[\cancelto{0}{-\sin\theta_0} - \sin n\triangle\theta]\\ \delta_n = \frac{2\pi}{\lambda}[-x\sin(n\triangle\theta)]\\ \theta_nr = n\triangle \theta r $
$ P_{avg} = \frac{1}{2}Re[E\times H^*] = \frac{1}{2n_0}|E|^2 = NE_0^2 +2E_0^2\sum_n\cos\bigg(\frac{2\pi}{\lambda}x[\sin\theta_n - \sin\theta_{n-1}] +(\omega_n-\omega_{n-1})t\bigg) $
$ \begin{align*} \text{Peak } &= NE_0 + 2NE_0\\ &= 3E_0N \end{align*} $
$ \begin{align*} \sin\theta_n - \sin\theta_{n-1} &= \sin(n\triangle \theta) - \sin(n\triangle \theta -\triangle \theta)\\ &= \sin(n\triangle \theta) - \sin(n\triangle \theta)\cos(\triangle\theta) +\sin(\triangle \theta)\cos(n\triangle \theta)\\ &\approx \sin(n\triangle \theta) - \sin(\triangle \theta)\big[1-\frac{\triangle \theta^2}{2}\big] + \triangle\theta\cos(n\triangle\theta)\\ &\approx \triangle\theta\bigg[\frac{\triangle\theta}{2} + \cos(n\triangle\theta)\bigg] \approx1+ \frac{\triangle \theta^2}{2}-\frac{\triangle \theta^3}{2} \end{align*} $
$ \cos\big(\frac{2\pi x}{\Omega}\big)\\ \Omega \approx \frac{\lambda}{1+ \frac{\triangle \theta^2}{2}-\frac{\triangle \theta^3}{2}} \\ $
not full/good solution