Questions

All questions are in this link

Solutions of all questions

1) $ \nabla\times\bar{E} = -\frac{\partial B}{\partial t}\hspace{0.5cm} \nabla\times\bar{H} =\frac{\partial \bar{D}}{\partial t}\hspace{0.5cm} \nabla \cdot\bar{D} =0\hspace{0.5cm} \nabla \cdot\bar{B} =0\\ $

a)

$ \nabla\times\nabla\times\bar{E} = -\frac{\partial}{\partial t}(\nabla \times\bar{B}) = -\mu_0\frac{\partial}{\partial t}\bigg(\frac{\partial D}{\partial t}\bigg) =-\mu_0\epsilon_0\frac{\partial\bar{E}}{\partial t^2} \\ \nabla^2 \bar{E} = \nabla\cancelto{0}{(\nabla\cdot \bar{E})} - \nabla\times\nabla\times\bar{E} \to \text{ using } \nabla\cdot\epsilon_0\bar{E}=0\\ \nabla\times\nabla\times\bar{E} = -\nabla^2\bar{E}\\ \nabla^2\bar{E} -\mu_0\epsilon_0\frac{\partial^2E}{\partial t^2} =0\\ $

b)

$ \nabla^2\bar{E}e^{j\omega t} - \mu_0\epsilon_0\frac{\partial^2}{\partial t^2}\bar{E}e^{j\omega t} =0\\ \nabla^2\bar{E}e^{j\omega t} - \mu_0\epsilon_0(-\omega^2)\bar{E}e^{j\omega t} =0\\ \nabla^2\bar{E} + (\omega^2\mu_0\epsilon_0) \bar{E} =0\\ \bar{E} =\hat{y} E_0e^{+j(\omega t -\beta z)}\hspace{0.5cm}\beta=\omega\sqrt{\mu_0\epsilon_0}\\ \bar{H} =\hat{x} \frac{E_0}{n_0}e^{j(\omega t -\beta z)}\hspace{0.5cm} n_0 = \sqrt{\frac{\mu_0}{\epsilon_0}}\\ $

\underline{side note:} $ \triangle\omega t -\triangle\beta z = \text{constant}\\ \triangle\omega -\triangle\beta \frac{\partial z}{\partial t} =0\\ \frac{dz}{dt} = \frac{\triangle \omega}{\triangle \beta}= \bigg(\frac{\partial\beta}{\partial\omega}\bigg)^{-1} = \sqrt{y} $

c)

$ \omega t -\beta z = constant\\ \omega - \beta \frac{dz}{dt} = 0\\ \frac{dz}{dt} = \frac{\omega}{\beta}\to v_p = \frac{\omega}{\beta} = \frac{1}{\sqrt{\mu_0\epsilon_0}} = c \to \text{dispersionless; does not depend on frequency}\\ $

2)

a)

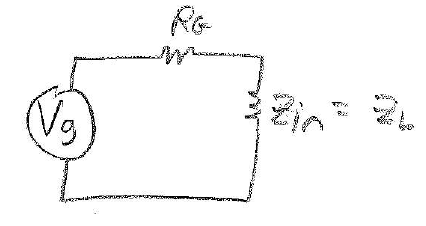
$ Z_{in} = Z_0\frac{Z_L + Z_0j\tan(\beta l)}{Z_0 + Z_1j\tan(\beta l)}\hspace{0.5cm}\beta l =\frac{2\pi}{\lambda}\bigg(\frac{\lambda}{4}\bigg)= \frac{\pi}{2}=\hspace{0.5cm}\tan\bigg(\frac{\pi}{2}\bigg)= \infty\\ Z_{in} = \frac{Z_0^2}{Z_L} = \frac{Z_0^2}{Z_0/2} = 2Z_0 \\ \text{\underline{want}: }Z_Q//Z_{in} = Z_0 =\frac{1}{\frac{1}{Z_q} +\frac{1}{2Z_0}}\hspace{1cm}\Gamma = \frac{Z_{in} - Z_0}{Z_{in}+Z_0}\\ \frac{1}{Z_q} +\frac{1}{2Z_0} =\frac{1}{Z_0}\\ \frac{1}{Z_q} = \frac{1}{2Z_0}\\ Z_q = 2Z_0\\ $

b) $ V(x) = V_0^+e^{-j\gamma x} + V_0^-e^{+j\gamma x}\\ \beta l =\frac{2\pi}{\lambda}\bigg(2\frac{3}{4}\lambda\bigg)=3\pi\hspace{1cm}\tan(3\pi) = \tan(\pi) = 0\\ Z_{in} = Z_0\frac{Z_L + Z_0j\tan(\beta l)}{Z_0 + Z_1j\tan(\beta l)} = Z_L = R_L = 0\\ \text{then } V(x) = 0\\ $

c)

for $ Z_{in} = Z_L: \tan(\beta l)=0\hspace{1cm}L<<\lambda $ \\ $ \beta l = \frac{2\pi}{\lambda}(l) = n\pi $ where $ n = 0,1,2,... $\\ $ l = \frac{n\lambda}{2} $\\

frequency must be low (no radiation) such that we only have TEM modes propagating.

3)

a)

$ \omega^2\mu\epsilon = \bigg(\frac{\pi m}{a}\bigg)^2 + \bigg(\frac{\pi n}{b}\bigg)^2\\ \left\{ \begin{array}{ll} a=0.015m\\ b=0.0075m\\ TE_{10} \text{ lowest mode (excited mode, depends on excitation method)} \end{array} \right.\\ f_c = \frac{1}{2\sqrt{\mu_0\epsilon_0}}\sqrt{\bigg(\frac{m}{a}\bigg)^2 + \bigg(\frac{n}{b}\bigg)^2}\\ f_c = \frac{c}{2}\bigg(\frac{1}{a}\bigg) = \frac{3\cdot10^8}{0.03} = 10^{10}\frac{1}{5} = 10GHz\\ $

b)

$ \beta =k\sqrt{1-\bigg(\frac{f_c}{f}\bigg)^2} = \omega\sqrt{\mu_0\epsilon_0}\sqrt{1-\bigg(\frac{f_c}{f}\bigg)^2}\\ =\sqrt{\omega^2\mu_0\epsilon_0 - (2\pi f)^2\mu_0\epsilon_0\bigg(\frac{f_c}{f}\bigg)^2} = \sqrt{\omega^2\mu_0\epsilon_0 - (2\pi)^2\mu_0\epsilon_0f_c^2} \\ $

$ \begin{align*} \beta^2&=k^2-k_c^2\\ k_c^2&=k_x^2+k_y^2\\ k_x &= \frac{m\pi}{a}\\ k_y &= \frac{n\pi}{b} \end{align*} \\ \beta = \sqrt{\omega^2\mu_0\epsilon_0 - \bigg(\frac{m\pi}{a}\bigg)^2 - \bigg(\frac{n\pi}{b}\bigg)^2}\\ $

c)

$ H_z(x,y,z) = H_z^0(x,y)e^{-j\beta z} \hspace{0.5cm}TE \\ $

BCs: $ \frac{\delta H_z}{\delta x}|_{x=0} = 0\hspace{0.5cm} \frac{\delta H_z}{\delta y}|_{y=0} = 0 \\ \frac{\delta H_z}{\delta x}|_{x=a} = 0\hspace{0.5cm} \frac{\delta H_z}{\delta y}|_{y=b} = 0 \\ \bar{H}_z = H_0 \cos\bigg(\frac{m\pi x}{a}\bigg)\cos\bigg(\frac{n\pi y}{b}\bigg)\cos(\omega t - \beta z) \\ $

d)

$ \omega_1 < 2\pi f_c<\omega_2\\ E_0 \cos(\omega_1t)\cos(\omega_2t) = \frac {E_0}{2}\{\cos[(\omega_1-\omega_2)t] + \cos[(\omega_1+\omega_2)t]\}\\ $

$ |\omega_1-\omega_2| =|9\pi\cdot10^9| \hspace{0.5cm}|\omega_1+\omega_2| = 29\pi\cdot10^9 \to $ both will pass through; no affect on the modulation frequency

Back to ECE Qualifying Exams (QE) page