Answers and Discussions for
Contents
[hide]Problem 3
Contemplation
The first step is to ponder the inductance matrix in $ \vec{\lambda}_{abs} = \mathbf{L}_s \vec{i}_{abs} $.
$ \begin{equation} \mathbf{L}_s = \begin{bmatrix} L_{asas} & L_{asbs} \\ L_{bsas} & L_{bsbs} \end{bmatrix} = \begin{bmatrix} 8 - 4\cos(2\theta_r) & -2\sin(2\theta_r) \\ -2\sin(2\theta_r) & 2 + \cos(2\theta_r) \end{bmatrix} \end{equation} $
Because the self-inductances change with rotor position $ \theta_r $, it is clear that some type of 2-phase, salient synchronous machine is the device under test. The self-inductances can be fit to a known general form.
$ \begin{align} L_{asas} &= L_{\ell as} + L_{Aas} + L_{Bas} \cos\left[2\left(\theta_r - 0\right)\right] = L_{\ell as} + L_{Aas} + L_{Bas} \cos\left(2\theta_r\right) \\ L_{bsbs} &= L_{\ell bs} + L_{Abs} + L_{Bbs} \cos\left[2\left(\theta_r - \frac{\pi}{2}\right)\right] = L_{\ell bs} + L_{Abs} - L_{Bbs} \cos\left(2\theta_r\right) \end{align} $
Phase Variable Referral
Something is amiss because the constant terms of the self-inductances are not equal: $ L_{\ell as} + L_{Aas} \neq L_{\ell bs} + L_{Abs} $ or $ 8 \, \textrm{H} \neq 2 \, \textrm{H} $. This would imply that the sinusoidal amplitudes of the winding functions are not equal for both windings. Before any calculations can proceed further, the machine has to be symmetrized through referred variables. The $ \mathit{bs} $-phase variables will be referred to the $ \mathit{as} $-phase variables.
$ \begin{align} \frac{N_a}{N_b} &= \sqrt{\frac{L_{\ell as} + L_{Aas}}{L_{\ell bs} + L_{Abs}}} = \sqrt{\frac{8}{2}} = 2 \\ \lambda_{bs}^{'} &= \frac{N_a}{N_b} \lambda_{bs} = 2 \lambda_{bs} \\ i_{bs}^{'} &= \frac{N_b}{N_a} i_{bs} = \frac{1}{2} i_{bs} \\ \mathbf{L}_s^{'} &= \begin{bmatrix} L_{asas} & L_{asbs}^{'} \\ L_{asbs}^{'} & L_{bsbs}^{'} \end{bmatrix} = \begin{bmatrix} L_{asas} & \frac{N_a}{N_b} L_{asbs} \\ \frac{N_a}{N_b} L_{asbs} & \left(\frac{N_a}{N_b}\right)^2 L_{bsbs} \end{bmatrix} = \begin{bmatrix} L_{asas} & 2 L_{asbs} \\ 2 L_{asbs} & 4 L_{bsbs} \end{bmatrix} \end{align} $
Thus, the referred inductance matrix is found. Notice that it is still a symmetric matrix and that the constant terms and the coefficient of the trigonometric function of $ 2\theta_r $ match respectively.
$ \begin{equation} \mathbf{L}_s^{'} = \begin{bmatrix} 8 - 4\cos(2\theta_r) & -4\sin(2\theta_r) \\ -4\sin(2\theta_r) & 8 + 4\cos(2\theta_r) \end{bmatrix} \end{equation} $
Drawing a Diagram
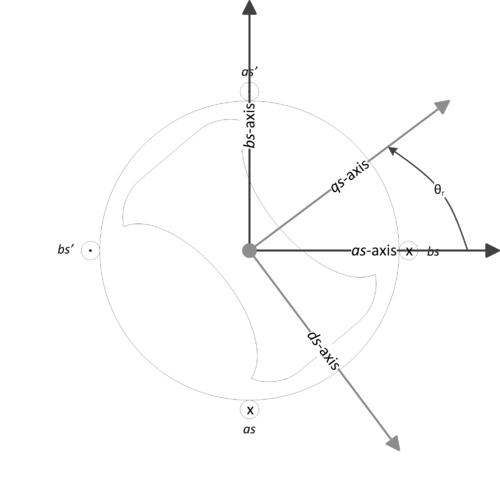
Now, the position-dependent behavior of the self-inductances is analyzed so that a diagram of the machine can be drawn with the $ \mathit{qs} $-axis and $ \mathit{ds} $-axis drawn correctly on the dogbone rotor and correct orientation at $ \theta_r = 0 $.
| $ \theta_r $ | $ 0^\circ $ | $ 45^\circ $ | $ 90^\circ $ | $ 135^\circ $ |
|---|---|---|---|---|
| $ L_{asas}(\theta_r) $ | min | ave | max | ave |
| $ L_{bsbs}(\theta_r) $ | max | ave | min | ave |
Orientation of the rotor can be determined from this table.
| $ \theta_r $ | $ 0^\circ $ | $ 45^\circ $ | $ 90^\circ $ | $ 135^\circ $ |
|---|---|---|---|---|
| $ \mathit{as} $-axis observes | mostly air | rotor corners | mostly steel | rotor corners |
| $ \mathit{bs} $-axis observes | mostly steel | rotor corners | mostly air | rotor corners |
It takes $ 90^\circ $ to go from mostly air to mostly steel, so there are only $ P = 2 $ poles on the machine, so the $ \mathit{ds} $-axis is $ \frac{2}{P} 90^\circ $ behind the $ \mathit{qs} $-axis. At $ \theta_r = 0^\circ $, the $ \mathit{qs} $-axis and $ \mathit{as} $-axis are aligned since the $ \mathit{qs} $-axis points out of the rotor where mostly air would be observed. A diagram can be made.
Finding Reference Frame Transformation
The reference frame transformation is going to be a type of rotor reference frame transformation in order to remove the $ \theta_r $ dependence from $ \mathbf{L}_s^{'} $. The general reference frame transformation is given below.
$ \begin{equation} \vec{f}_{qds}^r = \mathbf{K}_s^r \vec{f}_{abs}^{'} = \begin{bmatrix} K_{qsas}^r & K_{qsbs}^r \\ K_{dsas}^r & K_{dsbs}^r \end{bmatrix} \vec{f}_{abs}^{'} \end{equation} $
Each entry in the reference frame transformation matrix can be found using direction cosines, the cosine of the positive or negative angular distance through which the axis of the old coordinate system would have to be rotated through in order to coincide with the axis of the new coordinate system. The diagram should be used for reference.
- $ K_{qsas}^r $: The $ \mathit{as} $-axis should be rotated counterclockwise by $ \theta_r $ to align with the $ \mathit{qs} $-axis. $ K_{qsas}^r = \cos\left(\theta_r\right) $
- $ K_{qsbs}^r $: The $ \mathit{bs} $-axis should be rotated clockwise $ \frac{\pi}{2} $ radians (brought to the $ \mathit{as} $-axis), then rotated counterclockwise by $ \theta_r $ to align with the $ \mathit{qs} $-axis. $ K_{qsbs}^r = \cos\left(\theta_r - \frac{\pi}{2}\right) = \sin\left(\theta_r\right) $
- $ K_{dsas}^r $: The $ \mathit{as} $-axis should be rotated counterclockwise by $ \theta_r $ (brought to the $ \mathit{qs} $-axis), then rotated clockwise by $ \frac{\pi}{2} $ radians to align with the $ \mathit{ds} $-axis. $ K_{dsas}^r = \cos\left(\theta_r - \frac{\pi}{2}\right) = \sin\left(\theta_r\right) $
- $ K_{dsbs}^r $: The $ \mathit{bs} $-axis should be rotated clockwise $ \pi $ radians, then rotated counterclockwise by $ \theta_r $ to align with the $ \mathit{ds} $-axis. $ K_{dsbs}^r = \cos\left(\theta_r - \pi\right) = -\cos\left(\theta_r\right) $
The transformation is summarized in the matrix below.
$ \begin{equation} \boxed{\mathbf{K}_s^r = \begin{bmatrix} +\cos(\theta_r) & \sin(\theta_r) \\ \sin(\theta_r) & -\cos(\theta_r) \end{bmatrix}} \end{equation} $
Use Derived Transformation
To move from stator phase variables to the derived rotor reference frame, pre-multiply by $ \mathbf{K}_s^r =\begin{bmatrix} +\cos(\theta_r) & \sin(\theta_r) \\ \sin(\theta_r) & -\cos(\theta_r) \end{bmatrix} $. To do the opposite and move from the derived rotor reference frame to stator phase variables, pre-multiply by $ \mathbf{K}_r^s = \left(\mathbf{K}_s^r\right)^{-1} = \frac{1}{\cancelto{-1}{-\cos^2(\theta_r) - \sin^2(\theta_r)}} \begin{bmatrix} -\cos(\theta_r) & -\sin(\theta_r) \\ -\sin(\theta_r) & +\cos(\theta_r) \end{bmatrix} = \begin{bmatrix} +\cos(\theta_r) & \sin(\theta_r) \\ \sin(\theta_r) & -\cos(\theta_r) \end{bmatrix} = \mathbf{K}_s^r $. The inverse matrix is found with the explicit formula the the inverse of a 2x2 matrix and its determinant as well. (By coincidence, $ \mathbf{K}_s^r $ is an involutary matrix.)
The transformation of the flux linkage equations proceeds.
$ \begin{align} \vec{\lambda}_{qds}^{r} &= \mathbf{K}_s^r \vec{\lambda}_{abs}^{'} \\ \vec{\lambda}_{qds}^{r} &= \mathbf{K}_s^r \mathbf{L}_s^{'} \mathbf{K}_r^s \vec{i}_{qds}^{r} \\ \vec{\lambda}_{qds}^{r} &= \begin{bmatrix} +\cos(\theta_r) & \sin(\theta_r) \\ \sin(\theta_r) & -\cos(\theta_r) \end{bmatrix} \begin{bmatrix} 8 - 4\cos(2\theta_r) & -4\sin(2\theta_r) \\ -4\sin(2\theta_r) & 8 + 4\cos(2\theta_r) \end{bmatrix} \begin{bmatrix} +\cos(\theta_r) & \sin(\theta_r) \\ \sin(\theta_r) & -\cos(\theta_r) \end{bmatrix} \vec{i}_{qds}^{r} \\ \vec{\lambda}_{qds}^{r} &= \begin{bmatrix} 8\cos(\theta_r) - 4\cos(\theta_r)\cos(2\theta_r) - 4\sin(\theta_r)\sin(2\theta_r) & -4\cos(\theta_r)\sin(2\theta_r) + 8\sin(\theta_r) + 4\sin(\theta_r)\cos(2\theta_r) \\ 8\sin(\theta_r) - 4\sin(\theta_r)\cos(2\theta_r) + 4\cos(\theta_r)\sin(2\theta_r) & -4\sin(\theta_r)\sin(2\theta_r) - 8\cos(\theta_r) - 4\cos(\theta_r)\cos(2\theta_r) \end{bmatrix} \begin{bmatrix} +\cos(\theta_r) & \sin(\theta_r) \\ \sin(\theta_r) & -\cos(\theta_r) \end{bmatrix} \vec{i}_{qds}^{r} \end{align} $
The matrix has gotten so out of hand that reverting back to separated flux linkage equations helps fit the equation on the display.
$ \begin{align} \lambda_{qs}^r &= \begin{split} &{} \left[8\cos^2(\theta_r) - 4\cos^2(\theta_r)\cos(2\theta_r) - 4\sin(\theta_r)\cos(\theta_r)\sin(2\theta_r) - 4\sin(\theta_r)\cos(\theta_r)\sin(2\theta_r) + 8\sin^2(\theta_r) + 4\sin^2(\theta_r)\cos(2\theta_r)\right] i_{qs}^r \\ &{}+ \left[8\sin(\theta_r)\cos(\theta_r) - 4\sin(\theta_r)\cos(\theta_r)\cos(2\theta_r) - 4\sin^2(\theta_r)\sin(2\theta_r) + 4\cos^2(\theta_r)\sin(2\theta_r) - 8\sin(\theta_r)\cos(\theta_r) - 4\sin(\theta_r)\cos(\theta_r)\cos(2\theta_r)\right] i_{ds}^r \end{split} \\ \lambda_{qs}^r &= \begin{split} &{} \left[8\left(\sin^2(\theta_r) + \cos^2(\theta_r)\right) - 4\left(2\sin(\theta_r)\cos(\theta_r)\right)\sin(2\theta_r) - 4\left(\cos^2(\theta_r) - \sin^2(\theta_r)\right)\cos(2\theta_r)\right] i_{qs}^r \\ &{}+ \left[-4\left(2\sin(\theta_r)\cos(\theta_r)\right)\cos(2\theta_r) + 4\left(\cos^2(\theta_r) - \sin^2(\theta_r)\right)\sin(2\theta_r)\right] i_{ds}^r \end{split} \\ \lambda_{qs}^r &= \left[8 - 4\sin(2\theta_r)\sin(2\theta_r) - 4\cos(2\theta_r)\cos(2\theta_r)\right] i_{qs}^r + \left[-4\sin(2\theta_r)\cos(2\theta_r) - 4\cos(2\theta_r)\sin(2\theta_r)\right] i_{ds}^r \\ \lambda_{qs}^r &= 4\left[2 - \left(\sin^2(2\theta_r) + \cos^2(2\theta_r)\right)\right] i_{qs}^r + \left[0\right] i_{ds}^r \\ \lambda_{qs}^r &= 4\left[2 - 1\right] i_{qs}^r \\ \lambda_{qs}^r &= 4 i_{qs}^r \end{align} $
$ \begin{align} \lambda_{ds}^r &= \begin{split} &{} \left[8\sin(\theta_r)\cos(\theta_r) - 4\sin(\theta_r)\cos(\theta_r)\cos(2\theta_r) + 4\cos^2(\theta_r)\sin(2\theta_r) - 4\sin^2(\theta_r)\sin(2\theta_r) - 8\sin(\theta_r)\cos(\theta_r) - 4\sin(\theta_r)\cos(\theta_r)\cos(2\theta_r)\right] i_{qs}^r \\ &{}+ \left[8\sin^2(\theta_r) - 4\sin^2(\theta_r)\cos(2\theta_r) + 4\sin(\theta_r)\cos(\theta_r)\sin(2\theta_r) + 4\sin(\theta_r)\cos(\theta_r)\sin(2\theta_r) + 8\cos^2(\theta_r) + 4\cos^2(\theta_r)\cos(2\theta_r)\right] i_{ds}^r \end{split} \\ \lambda_{ds}^r &= \left[0\right] i_{qs}^r + \left[8\left(\sin^2(\theta_r) + \cos^2(\theta_r)\right) + 4\left(2\sin(\theta_r)\cos(\theta_r)\right)\sin(2\theta_r) + 4\left(\cos^2(\theta_r) - \sin^2(\theta_r)\right)\cos(2\theta_r)\right] i_{ds}^r \\ \lambda_{ds}^r &= \left[8 + 4\sin(2\theta_r)\sin(2\theta_r) + 4\cos(2\theta_r)\cos(2\theta_r)\right] i_{ds}^r \\ \lambda_{ds}^r &= 4\left[2 + \left(\sin^2(2\theta_r) + \cos^2(2\theta_r)\right)\right] i_{ds}^r \\ \lambda_{ds}^r &= 4\left[2 + 1\right] i_{ds}^r \\ \lambda_{ds}^r &= 12 i_{ds}^r \end{align} $
These trigonometric simplifications rely on the Pythagorean Identity of $ \sin^2(x) + \cos^2(x) = 1 $ (not given), the Double Angle Identity for sine of $ \sin(2x) = 2\sin(x)\cos(x) $ (derived from given), and the Double Angle Identity for cosine of $ \cos(2x) = \cos^2(x) - \sin^2(x) $ (derived from given). All rotor position dependence has been removed from the equations as was initially sought back at the start of the solution. The vector flux linkage equation is finished.
$ \begin{equation} \boxed{\vec{\lambda}_{qds}^r = \begin{bmatrix} 4 & 0 \\ 0 & 12 \end{bmatrix} \vec{i}_{qds}^r} \end{equation} $
Discussion
Michael Hayashi on 17 January 2018
- This problem is ridiculous. Referring one stator phase to another is rarely asked and just delays someone from getting to the crux of the problem. The diagram can be constructed from there, and the transformation matrix follows in relatively short order. The most exacting part of the problem is actually proving that the transformation works because multiplying three matrices with trigonometric functions for each entry is absurdly tedious for a timed exam under any circumstances. The exam author does not even do the favor of giving the Double Angle Identities directly, instead inserting another delay by offering the more general Angle Sum and Difference Identities. Any mathematical error would prove disastrous to finishing on time.
- A shortcut could be made by substituting $ L_{A} = L_{Aas} = L_{Abs}^{'} = 8 $ and $ L_{B} = L_{Bas} = L_{Bbs}^{'} = -4 $ from the general form of self-inductance (assuming no leakage inductance) into magnetizing inductance equations for a two-phase machine: $ L_{mq} = \left(L_{A} + L_{B}\right) = 4 $ and $ L_{md} = \left(L_{A} - L_{B}\right) = 12 $. This would assume that the transformation matrix was chosen correctly, thus each reference frame inductance was fully decoupled and made rotor position-independent. Would this even get full points? The given hints of trigonometric identities would suggest that the grader is looking for the transformation math to be worked out.