Communication, Networking, Signal and Image Processing (CS)
Question 1: Probability and Random Processes
January 2006
1 (33 points)
Let $ \mathbf{X} $ and $ \mathbf{Y} $ be two joinly distributed random variables having joint pdf
$ f_{\mathbf{XY}}\left(x,y\right)=\left\{ \begin{array}{lll} 1, & & \text{ for }0\leq x\leq1\text{ and }0\leq y\leq1\\ 0, & & \text{ elsewhere. } \end{array}\right. $
(a)
Are $ \mathbf{X} $ and $ \mathbf{Y} $ statistically independent? Justify your answer.
$ f_{\mathbf{X}}\left(x\right)=\int_{-\infty}^{\infty}f_{\mathbf{XY}}\left(x,y\right)dy=\int_{0}^{1}dy=1\text{ for }0\leq x\leq1. $
$ f_{\mathbf{Y}}\left(y\right)=\int_{-\infty}^{\infty}f_{\mathbf{XY}}\left(x,y\right)dx=\int_{0}^{1}dx=1\text{ for }0\leq y\leq1. $
Since $ f_{\mathbf{XY}}\left(x,y\right)=f_{\mathbf{X}}\left(x\right)f_{\mathbf{Y}}\left(y\right) $ , $ \mathbf{X} $ and $ \mathbf{Y} $ are $ statistically independent. $
(b)
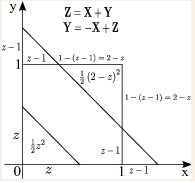
Let $ \mathbf{Z} $ be a new random variable defined as $ \mathbf{Z}=\mathbf{X}+\mathbf{Y} $ . Find the cdf of $ \mathbf{Z} $ .
$ F_{\mathbf{Z}}\left(z\right)=P\left(\left\{ \mathbf{Z}\leq z\right\} \right)=P\left(\left\{ \mathbf{X}+\mathbf{Y}\leq z\right\} \right). $
• i) if $ z<0 $ , then $ F_{\mathbf{Z}}\left(z\right)=0 $ .
• ii) if $ z\geq2 $ , then $ F_{\mathbf{Z}}\left(z\right)=1 $ .
• iii) if $ 0\leq z\leq1 $ , then $ F_{\mathbf{Z}}\left(z\right)=\iint f_{\mathbf{XY}}\left(x,y\right)dxdy=\iint1\cdot dxdy=\frac{1}{2}z^{2} $ .
• iv) if $ 1<z<2 $ , then $ F_{\mathbf{Z}}=\iint f_{\mathbf{XY}}\left(x,y\right)dxdy=\iint1\cdot dxdy=1-\frac{1}{2}\left(2-z\right)^{2} $ .
$ \therefore F_{\mathbf{Z}}\left(z\right)=\left\{ \begin{array}{lll} 0 & & ,z<0\\ \frac{1}{2}z^{2} & & ,0\leq z\leq1\\ 1-\frac{1}{2}\left(2-z\right)^{2} & & ,1<z<2\\ 1 & & ,z\geq2 \end{array}\right. $
(c)
Find the variance of $ \mathbf{Z} $ .
$ f_{\mathbf{Z}}\left(z\right)=\left\{ \begin{array}{lll} z & & ,0\leq z\leq1\\ 2-z & & ,1<z<2\\ 0 & & \text{,otherwise.} \end{array}\right. $
$ E\left[\mathbf{Z}\right]=\int_{-\infty}^{\infty}z\cdot f_{\mathbf{Z}}\left(z\right)dz=\int_{0}^{1}z^{2}dz+\int_{1}^{2}\left(2z-z^{2}\right)dz=\frac{1}{3}z^{3}\Bigl|_{0}^{1}+z^{2}-\frac{1}{3}z^{3}\Bigl|_{1}^{2}=\frac{1}{3}+3-\frac{7}{3}=1. $ $ E\left[\mathbf{Z}^{2}\right]=\int_{-\infty}^{\infty}z^{2}\cdot f_{\mathbf{Z}}\left(z\right)dz=\int_{0}^{1}z^{3}dz+\int_{1}^{2}\left(2z^{2}-z^{3}\right)dz=\frac{1}{4}z^{4}\Bigl|_{0}^{1}+\frac{2}{3}z^{3}-\frac{1}{4}z^{4}\Bigl|_{1}^{2}=\frac{1}{4}+\frac{14}{3}-\frac{15}{4}=\frac{7}{6}. $ $ Var\left[\mathbf{Z}\right]=E\left[\mathbf{Z}^{2}\right]-\left(E\left[\mathbf{Z}\right]\right)^{2}=\frac{1}{6}. $