Communication, Networking, Signal and Image Processing (CS)
Question 1: Probability and Random Processes
August 2002
1. (25 Points)
Consider a random experiment in which a point is selected at random from the unit square (sample space $ S=\left[0,1\right]\times\left[0,1\right] ) $. Assume that all points in $ S $ are equally likely to be selected. Let the random variable $ \mathbf{X}\left(\omega\right) $ be the distance from the outcome $ \omega $ to the origin (the lower left corner of the unit square). Find the cumulative distribution function (cdf) $ F_{\mathbf{X}}\left(x\right)=P\left(\left\{ \mathbf{X}\leq x\right\} \right) $ of the random variable $ \mathbf{X} $ . Make sure and specify your answer for all $ x\in\mathbf{R} $ .
Solution
$ F_{\mathbf{X}}\left(x\right)=P\left(\left\{ \mathbf{X}\leq x\right\} \right)=P\left(\left\{ w:\mathbf{X}\left(w\right)\leq x\right\} \right). $
• $ i)\; x<0,\; F_{\mathbf{X}}\left(x\right)=0 $
• $ ii)\;0\leq x\leq1,\; F_{\mathbf{X}}\left(x\right)=\frac{\pi}{4}x^{2} $
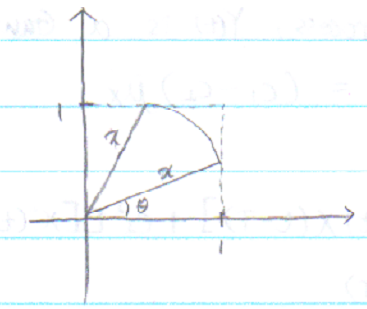
• $ iii)\;1<x<\sqrt{2}, F_{\mathbf{X}}\left(x\right)=2\left(\frac{1}{2}\times1\times\sqrt{x^{2}-1}\right)+\pi x^{2}\times\frac{\frac{\pi}{2}-2\theta}{2\pi} $$ =\sqrt{x^{2}-1}+\frac{\pi}{4}x^{2}-\theta x^{2}=\sqrt{x^{2}-1}+\frac{\pi}{4}x^{2}-x^{2}\cos^{-1}\frac{1}{x} $$ =\sqrt{x^{2}-1}+\left(\frac{\pi}{4}-\cos^{-1}\frac{1}{x}\right)x^{2}. $
• $ iv)\; x\geq\sqrt{2},\; F_{\mathbf{X}}\left(x\right)=1 $
$ \therefore\; F_{\mathbf{X}}\left(x\right)=\begin{cases} \begin{array}{lll} 0 & & ,\; x<0\\ \frac{\pi}{4}x^{2} & & ,\;0\leq x\leq1\\ \sqrt{x^{2}-1}+\left(\frac{\pi}{4}-\cos^{-1}\frac{1}{x}\right)x^{2} & & ,\;1<x<\sqrt{2}\\ 1 & & ,\; x\geq\sqrt{2}. \end{array}\end{cases} $