Computer Engineering(CE)
Question 1: Algorithms
August 2013
Back to QE CE question 2, August 2013
Problem 2.
Suppose your company develops and manages construction of boat launching docks along a downstream stretch of the Wabash river. This stretch runs north-south for $ L $ miles within the State of Indiana. The possible sites for docks are given by numbers $ x_1 < x_2 < x_3 < ... < x_n $, each in the interval $ [0,L] $, specifying their positions in miles measured from the northern end of this stretch of the Wabash river. If your company constructs a dock at position $ x_i $, it receives a revenue of $ r_i >0 $. Regulations imposed by the Indiana Department of Water Resource Management require that no two docks should be built within a distance of less than 5 miles from each other. Your company plans to construct docks at a subset of the potential sites so as to maximize the total revenue., subject to this distance restriction. For example, suppose $ L=20 $ and $ n=5 $ with potential sites given by $ \lbrace x_1, x_2, x_3, x_4, x_5 \rbrace = \lbrace 6,7,12,13,14\rbrace $ and $ \lbrace r_1, r_2, r_3, r_4, r_5 \rbrace = \lbrace 5,6,5,3,1\rbrace $. Then the best solution is to construct docks at locations $ x_1 $ and $ x_3 $ to achieve a revenue of 10. Describe a dynamic programming formulation to find a solution for this optimization problem. Compute the complexity of solving your dynamic programming formulation of this problem.
Share and discuss your solution below.
Solution 1
This problem can be solved using dynamic programming. For each dock $ x_i $, compute the revenue from $ x_1 $ to $ x_i $, if $ x_i $ is selected, and the revenue for remaining docks $ x_{i+1} $ to $ x_n $, if $ x_i $ is not selected.
$ R[i] $: denote the total revenue using only sites $ x_1, \dots , x_i $.
$ L[i] $: denote $ i $ with the greatest value such that $ x_i $ is used for the solution in $ R[i] $.
Initially, $ L[<=0]=0 $, $ R[<=0]=0 $, $ x_0 = -\infty $, $ r_0=0 $. The pseudo code for dynamic programming is showing below. Note we use bottom up to fill up $ R $ and $ L $.
In the end of the program, $ R[n] $ will be the maximum revenue, and $ L[n] $, $ L[L[n]] $, ... will be the indices of locations to choose.
Solution 2
Sub-problem: after picking one location $ q $, need to find the max revenue of the remaining docks whose location is greater than 5 miles away from $ q $. Bottom-up-dock-revenue.
Let $ r[0...n] $ be a new array, $ r[0]=0 $. The pseudo code is show below:
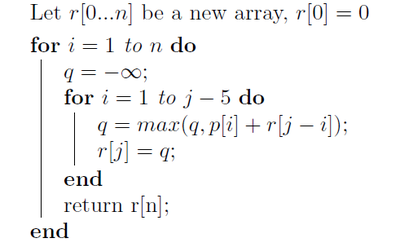
Comments on Solution 2:
Using dynamic program and bottom up to fill in the solution is a good approach.
For each dock, we need to find the greater of either selecting this dock and have the revenue for this dock, while any other docks within 5 miles will not be selected; or not selecting the dock and having the remaining docks that includes the docks within 5 miles away to achieve their best revenue. In this solution, it is not clear what $ p[i] $ is represent for. In addition, the docks what within 5 miles away could be on both sides. This solution only consider one side.


